▸ Ejercicios Resueltos de Selectividad→Análisis-Matemáticas Sociales

(245) ejercicios de Matemáticas PAU Andalucía

(22) ejercicios de Mat. C. Sociales II - Análisis (Funciones, Continuidad, Límites y Derivadas)

(#3380) - Selectividad Andalucía 2011-1-A2

Tras un test realizado a un nuevo modelo de automóvil, se ha observado que el consumo de gasolina, 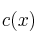$c(x)$ , expresado en litros, viene dado por la función

$c(x)=7.5-0.05x+0.00025x^2$

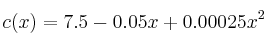
siendo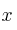 $x$ , la velocidad en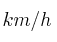 $km/h$

– a) Determine el consumo de gasolina a las velocidades de 50 km/h y 150 km/h.
– b) Estudie el crecimiento y decrecimiento de la función c(x) .
– c) ¿A qué velocidades de ese intervalo se obtiene el mínimo consumo y el máximo consumo y cuáles son éstos?
(#3406) - Selectividad Andalucía 2010-6-A2

Sea la función $f(x)=2x^2+ax+b$

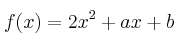
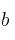– a) Determine los valores de $a$ y $b$ sabiendo que su gráfica pasa por el punto 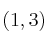$(1, 3)$ y alcanza un extremo local en el punto de abscisa $x=-2$ .
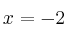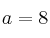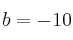– b) Tomando $a = 8$ y $b = -10$ deduzca la curvatura de su gráfica, el valor mínimo que alcanza la función y los valores donde la función se anula.
(#3675) - Selectividad Andalucía 2010-2-B2

El gerente de una empresa sabe que los beneficios de la misma, 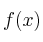$f(x)$ , dependen de la inversión, 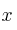$x$ , según la función 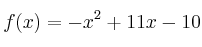$f(x)=-x^2+11x-10$ . (x es la cantidad invertida en millones de euros).

– a) Determine los valores de la inversión para los que la función beneficio es no negativa.
– b) Halle el valor de la inversión para el cual el beneficio es máximo. ¿A cuánto asciende éste?
– c) ¿Entre qué valores ha de estar comprendida la inversión para que el beneficio sea creciente, sabiendo que éste es no negativo?
(#3391) - Selectividad Andalucía 2010-1-A2
Ver solución en vídeo

En una empresa han hecho un estudio sobre la rentabilidad de su inversión en publicidad, y han llegado a la conclusión de que el beneficio obtenido, en miles de euros, viene dado por la expresión 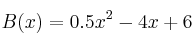$B(x) = 0.5x^2-4x+6$ , siendo x la inversión en publicidad, en miles de euros, con x en el intervalo $[0,10]$ .

– a) ¿Para qué valores de la inversión la empresa tiene pérdidas?
– b) ¿Cuánto tiene que invertir la empresa en publicidad para obtener el mayor beneficio posible?
– c) ¿Cuál es el beneficio si no se invierte nada en publicidad? ¿Hay algún otro valor de la inversión para el cual se obtiene el mismo beneficio?
(#3377) - Selectividad Andalucía 2007-6-A2

El beneficio obtenido por una empresa, en miles de euros, viene dado por la función

$f(x) = \left\{ \begin{array}{lcr} -5x^2+40x-60 & si & 0 \leq x \leq 6 \\ \\ \frac{5x}{2}-15 & si & 6 < x \leq 10 \\ \end{array} \right.$

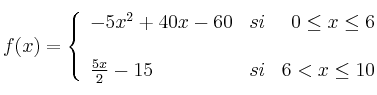
donde x representa el gasto en publicidad en miles de euros.

– a) Represente la función f .
– b) Calcule el gasto en publicidad a partir del cual la empresa no tiene pérdidas.
– c) ¿Para qué gastos en publicidad se producen beneficios nulos?
– d) Calcule el gasto en publicidad que produce máximo beneficio. ¿Cuál
es ese beneficio máximo?

Selectividad Andalucía

Matemáticas II

Mat. C. Sociales II