-
La concejalía de Educación de una determinada localidad afirma que el tiempo medio dedicado a la lectura por los jóvenes de entre 15 y 20 años de edad es, a lo sumo, de 8 horas semanales. Para contrastar esta hipótesis, (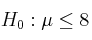
) se escoge al azar una muestra de 100 jóvenes, de entre 15 y 20 años, y se obtiene una media de 8.3 horas de dedicación a la lectura. Supuesto que el tiempo dedicado a la lectura sigue una ley Normal con desviación típica igual a 1 hora, ¿qué se puede decir, a un nivel de significación del 5%, sobre la afirmación de la concejalía?
-
Se desea tomar una muestra aleatoria estratificada de las personas mayores de edad de un municipio, cuyos estratos son los siguientes intervalos de edades, en años: de 18 a 30, de 31 a 45, de 46 a 60 y mayores de 60. En el primer intervalo hay 7500 personas, en el segundo hay 8400, en el tercero 5700 y en el cuarto 3000. Calcule el tamaño de la muestra total y su composición, sabiendo que el muestreo se hace con afijación proporcional y se han elegido al azar 375 personas del primer estrato.
-
De una población de 120 alumnos, hay 48 que tienen 2 o más hermanos. Si de dicha población se toman muestras de tamaño 40.
– a) ¿Qué distribución siguen las proporciones muestrales?.
– b) ¿Cuál es la probabilidad de que se encuentre en dicha muestra una proporción de más del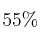 
de alumnos con 2 o más hermanos?.
-
Una cadena de supermercados desea estimar la proporción de clientes que adquiere un determinado producto. Para ello ha tomado una muestra aleatoria simple de 1000 clientes y ha observado que 300 compraban ese producto.
– a) Halle, con un nivel de confianza del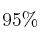 
, un intervalo de confianza para estimar la proporción de clientes del supermercado que compra ese producto.
– b) Si en otra muestra la proporción de clientes que compra ese producto es de 0.25 y el error cometido en la estimación ha sido inferior a 0.03, con un nivel de confianza del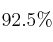 
, calcule el tamaño mínimo de la muestra.
-
Se quiere estimar la proporción de estudiantes que asiste de forma regular al cine. Para ello, se toma una muestra aleatoria simple de tamaño 300 y se obtiene que de ellos, 210 acuden con regularidad al cine.
– a) Calcule un intervalo de confianza al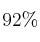 
para estimar la proporción de estudiantes que va al cine regularmente. ¿Qué error máximo se cometería si se diera como estimación de dicha proporción 0.7?
– b) Con el mismo nivel de confianza, siendo la proporción muestral la misma, si queremos que el error sea menor que 0.02, ¿cuántos alumnos como mínimo hay que elegir en la muestra?
