Ejercicios de Funciones y derivadas- Matemáticas Aplicadas a las C. S. II
(29) ejercicios de Funciones y Derivadas
-
Sea
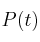 el porcentaje de células, de un determinado tejido, afectadas por un cierto tipo de enfermedad transcurrido un tiempo
el porcentaje de células, de un determinado tejido, afectadas por un cierto tipo de enfermedad transcurrido un tiempo 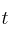 , medido en meses:
, medido en meses:
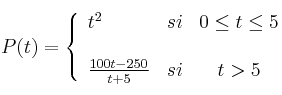
– a) Estudie la continuidad de la función P.
– b) Estudie la derivabilidad de P en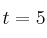 .
.
– c) Estudie la monotonía de dicha función e interprete la evolución del porcentaje de células afectadas.
– d) ¿En algún momento el porcentaje de células afectadas podría valer 50? -
El gerente de una empresa sabe que los beneficios de la misma,
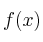 , dependen de la inversión,
, dependen de la inversión, 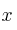 , según la función
, según la función 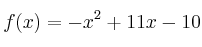 . (x es la cantidad invertida en millones de euros).
. (x es la cantidad invertida en millones de euros).– a) Determine los valores de la inversión para los que la función beneficio es no negativa.
– b) Halle el valor de la inversión para el cual el beneficio es máximo. ¿A cuánto asciende éste?
– c) ¿Entre qué valores ha de estar comprendida la inversión para que el beneficio sea creciente, sabiendo que éste es no negativo? -
En el mar hay una mancha producida por una erupción marina. La superficie afectada, en
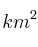 , viene dada por la función
, viene dada por la función 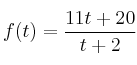 , siendo
, siendo 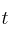 el tiempo transcurrido desde que empezamos a observarla.
el tiempo transcurrido desde que empezamos a observarla.– a) ¿Cuál es la superficie afectada inicialmente, cuando empezamos a medirla?
– b) Estudie si la mancha crece o decrece con el tiempo
– c) ¿Tiene algún límite la extensión de la superficie de la mancha? -
En una empresa de montajes el número de montajes diarios realizados por un trabajador depende de los días trabajados según la función
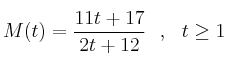 ,
,
donde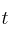 es el número de días trabajados.
es el número de días trabajados.– a) ¿Cuántos montajes realiza el primer día? ¿Cuántos días necesitará para
realizar cinco montajes diarios?
– b) ¿Qué ocurriría con el número de montajes diarios si trabajara indefinidamente?
– c) El dueño de la empresa cree que el número de montajes diarios aumenta con los días de trabajo. Estudiando la función, justifique si es cierta dicha creencia.
– d) Dibuje la gráfica de la función. -
– a) Halle la función derivada de la función
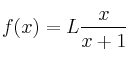 y simplifique el resultado.
y simplifique el resultado.
– b) Obtenga las asíntotas de la función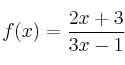
– c) Obtenga los intervalos de concavidad y convexidad de la función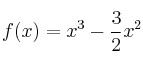
 Matemáticas IES
Matemáticas IES

