-
La Gran Pirámide de Guiza (también conocida como Pirámide de Keops o de Jufu) es la más antigua de las siete maravillas del mundo y la única que aún perdura, además de ser la mayor de las pirámides de Egipto. Ayúdanos a conocer un poco más de la Gran Pirámide, siguiendo los siguientes pasos:
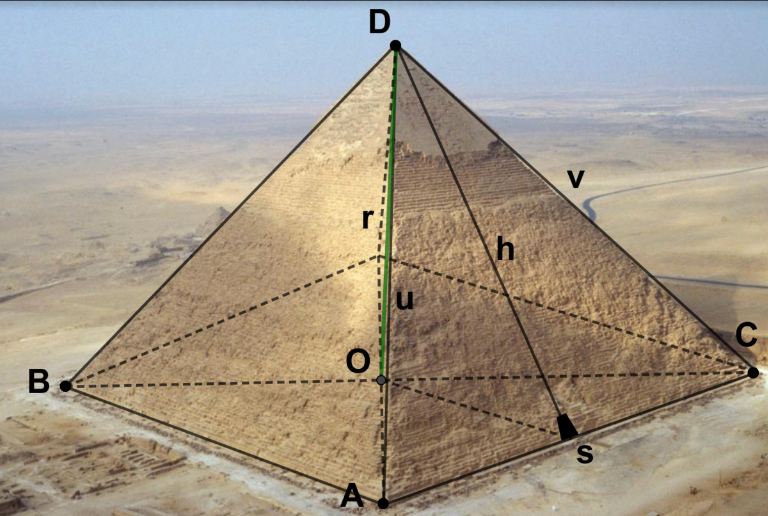
distancias
1) La base de la pirámide está formada por los cuatro puntos de los cuales tres puntos son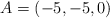 
, 
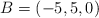y 
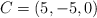. Forma los vectores 
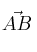y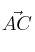 
, comprueba que son linealmente independientes y calcula el área del paralelogramo que forman haciendo uso del producto vectorial. Sabiendo que la longitud es 
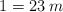y por tanto la superficie es 
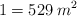¿Cuántos metros cuadrados de superficie tiene la Gran Pirámide?
2) Si la vertical del centro de la pirámide sigue esta ecuación:
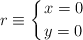
Y el lado de la puerta (donde está el 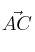) es la recta de ecuación:
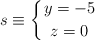
¿Cuántos metros hay de la puerta al centro de la pirámide, O? Demuéstralo con la distancia entre dos rectas (1=23 m)
3) Sabiendo que la cúspide (D) está en el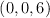 
calcular las ecuaciones vectoriales y paramétricas de las dos rectas 
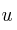y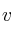 
que forma los lados (
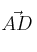y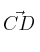 
)
4) Halla el plano que contiene a la puerta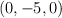 
y es un lado de la pirámide. Halla el plano que es vertical y contiene a la puerta y al centro O. Interseca ambos planos obteniendo la ecuación de la recta 
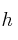. Comprueba que es la misma recta que pasa por la puerta y la cúspide D.
-
Considera las rectas
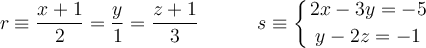
– a) Estudia y determina la posición relativa de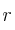 
y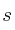 
– b) Calcula la distancia entre 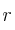y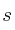
-
Considera la recta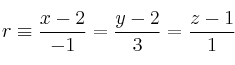 
y los planos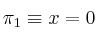 
y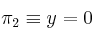 
– a) Halla los puntos de la recta 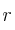que equidistan de los planos 
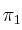y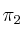 
– b) Determina la posición relativa de la recta 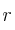y la recta de instersección de los planos 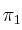y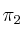
-
A la empresa de obras públicas North SA se le ha encargado la construcción de una autovía que una dos importantes ciudades andaluzas. El recorrido de la misma pasa por una montaña y por razones económicas se ha decidido atravesarla construyendo un túnel. Tú puedes echar una mano a los ingenieros implicados en el proyecto a la hora de afrontar los cálculos matemáticos necesarios para realizar la obra.
Se pide:
1. El túnel sigue la trayectoria marcada por los puntos A(-1,1,1) y B(1,2,1). Halla la recta que pasa por estos, a la cual vamos a llamar r.
2. Las laderas de la montaña vienen dadas por lo planos cuyas ecuaciones son:
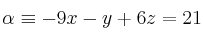y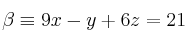 
Halla los puntos de intersección de la recta r con los planos, vamos a nombrar a estos puntos como E(entrada) y S(salida).
3. Halla la longitud del túnel (distancia entre E y S).
4. En la cima de la montaña se va a trazar otra carretera cuya trayectoria viene determinada por la intersección de los planos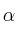 
y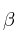 
. Halla la intersección de los mismos, a la cual vamos a llamar s.
5 Para la ventilación del túnel se va a crear un pozo de impulsión que conecta la cima de la montaña con el túnel y se quiere saber cuál es la longitud del mismo, el pozo sigue la perpendicular que une las rectas r y s. Halla la distancia entre ambas rectas.
-
Consideramos los puntos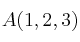 
, 
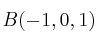y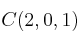 
.
– a) Calcula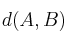 
(distancia entre los puntos A y B)
– b)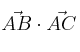 
(producto escalar)
– c) Calcula el perímetro del triángulo de vértices A, B y C
– d) Halla el área del triángulo de vértices A, B y C
Matemáticas IES
distancias