-
El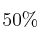 
de los préstamos que concede un banco son para vivienda, el 
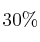para industria y el 
para consumo. No se pagan el de los préstamos para vivienda, el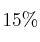 
de los préstamos para industria y el 
de los préstamos para consumo.
– a) Si se elige al azar un préstamo, calcule la probabilidad de que se pague.
– b) Se elige un préstamo al azar que resulta impagado, ¿cuál es la probabilidad de que sea un préstamo para consumo?
– c) Ante un préstamo impagado el director del banco afirma que es más probable que sea para vivienda que para consumo, ¿lleva razón el director?
-
Se cree que hay una vuelta hacia estilos de baile más populares, por lo que se realiza una encuesta a estudiantes de bachillerato, resultando que al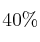 
les gusta la salsa, al 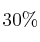les gusta el merengue y al 
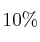les gusta tanto la salsa como el merengue.
– a) ¿Cuál es la probabilidad de que a un estudiante le guste el merengue si
le gusta la salsa?
– b) ¿Y la de que a un estudiante le guste el merengue si no le gusta la salsa?
– c) ¿Son independientes los sucesos “gustar la salsa” y “gustar el merengue”?
¿Son compatibles?
-
En un experimento aleatorio, la probabilidad de que ocurra un suceso A es 0.68, la de que ocurra otro suceso B es 0.2, y la de que no ocurra ninguno de los dos es 0.27. Halle la probabilidad de que:
– a) Ocurran los dos a la vez.
– b) Ocurra B pero no A.
– c) Ocurra B, sabiendo que no ha ocurrido A.
-
Un Centro de Salud propone dos terapias, A y B, para dejar de fumar. De las personas que acuden al Centro para dejar de fumar, el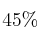 
elige la terapia A, y el resto la B. Después de un año el de los que siguieron la terapia A y el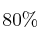 
de los que siguieron la B no han vuelto a fumar.
Se elige al azar un usuario del Centro que siguió una de las dos terapias:
– a) Calcule la probabilidad de que después de un año no haya vuelto a fumar.
– b) Si transcurrido un año esa persona sigue sin fumar, calcule la probabilidad de que hubiera seguido la terapia A.
– c) Si transcurrido un año esa persona ha vuelto a fumar, calcule la probabilidad de que hubiera seguido la terapia A
-
En una empresa de montajes el número de montajes diarios realizados por un trabajador depende de los días trabajados según la función
,
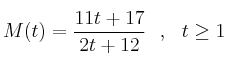donde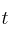 
es el número de días trabajados.
– a) ¿Cuántos montajes realiza el primer día? ¿Cuántos días necesitará para
realizar cinco montajes diarios?
– b) ¿Qué ocurriría con el número de montajes diarios si trabajara indefinidamente?
– c) El dueño de la empresa cree que el número de montajes diarios aumenta con los días de trabajo. Estudiando la función, justifique si es cierta dicha creencia.
– d) Dibuje la gráfica de la función.
Matemáticas IES
Matemat_Soc_Andalucía_2013
andalucía