Ejercicios de Funciones y derivadas- Matemáticas Aplicadas a las C. S. II

(29) ejercicios de Funciones y Derivadas

  • (#4225)      Ver Solución Seleccionar

    Calcula las derivadas de las siguientes funciones usando las reglas de derivación:

    – f(x)=\frac{3x}{x^2-9}
    – f(x)=3x^2-5x+6
    – f(x)=Ln(x+2)
    – f(x)=5x \cdot 2^x
    – f(x)=\sqrt{x+2}

  • (#4226)      Ver Solución Seleccionar

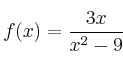
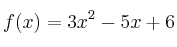
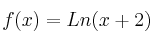
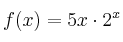
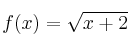
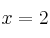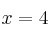    Calcula las integrales de las siguientes funciones entre x=2 y x=4 aplicando la regla de Barrow:

    – f(x)=x^5
    – f(x)=3x^2-5x+6
    – f(x)=\frac{-1}{2x}
    – f(x)=2^x
    – f(x)=\sqrt{x+2}

  • (#2697)      Ver Solución Seleccionar

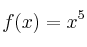
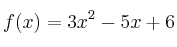
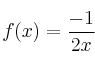
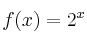
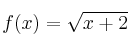
    El beneficio, en miles de euros, que ha obtenido una almazara a lo largo de 50 años de vida viene dado por la expresión B(t)=\left\{ \begin{array}{lr} -0.04t^2+2.4t & 0 \leq t < 40 \\ & \\ \frac{40t-320}{t} & 40 \leq t \leq 50 \end{array} \right.
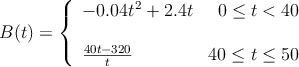
    donde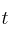 t es el tiempo transcurrido.

    – a) Estudie la continuidad y la derivabilidad de la función 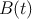B(t) en el intervalo [0,50].
    – b) Estudie la monotonía de la función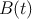 B(t) y determine en qué momento fueron mayores los beneficios de la almazara, así como el beneficio máximo.
    – c) Represente la gráfica de la función y explique la evolución del beneficio.

  • (#4398)      Ver Solución Seleccionar

    – a) Calcule la derivada de las funciones

    f(x)=e^{5x} \cdot (x^2-5)^3 \qquad \qquad g(x)=\frac{(x^3+1)^2}{ln(x^2+2)}

    – b) Obtenga la ecuación de la recta tangente a la gráfica de la función 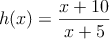h(x)=\frac{x+10}{x+5}, el punto de abscisa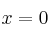 x=0

  • (#2745)      Ver Solución Seleccionar

    El consumo de cereales en una ciudad, en miles de toneladas, viene dado por la función 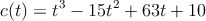c(t)=t^3-15t^2+63t+10, para 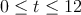0 \leq t \leq 12, donde 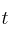t representa el tiempo.

    – a) ¿En qué instante se alcanza el máximo consumo de cereales y cuántas toneladas se consumen en ese momento?
    – b) ¿En qué intervalo de tiempo decrece el consumo de cereales?
    – c) Represente gráficamente la función.