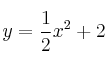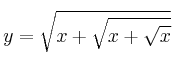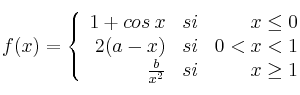EJERCICIOS RESUELTOS - Funciones, Derivadas e Integrales
Análisis matemático: Funciones, Límites, Derivadas e Integrales
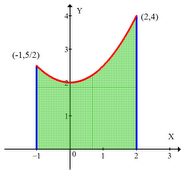
Calcula el área encerrada entre las curvas ![]() y
y ![]()
Halla el área encerrada entre las funciones ![]() y
y ![]()
Calcule máximos y mínimos de la función ![]()
Calcular la derivada de la función ![]()
Hallar dominio, continuidad y corte con los ejes de la función 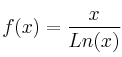
Dada la función ![]() , determinar los valores de
, determinar los valores de ![]() ,
, ![]() y
y ![]() si sabemos que
si sabemos que ![]() tiene un óptimo en
tiene un óptimo en ![]() y la pendiente de la recta tangente a
y la pendiente de la recta tangente a ![]() en
en ![]() es
es ![]() .
.
 Matemáticas IES
Matemáticas IES