EJERCICIOS RESUELTOS - Programación Lineal
Matemáticas Aplicadas a las Ciencias Sociales II (2º Bachillerato)
Un fabricante diseña pantalones y camisas. Para ello dispone de 50 metros de tejido de algodón y 124 metros de tejido de lino. Cada pantalón precisa 0.75 metros de algodón y 2 metros de lino. Para cada camisa se necesitan 0.5 metros de algodón y 1 metro de lino. El precio de mercado del pantalón es de 40 euros y el de la camisa de 25 euros. Se trata de encontrar el número de pantalones y camisas que debe diseñar el fabricante para obtener unos ingresos máximos.
a) Represente gráficamente la región determinada por las siguientes restricciones y determine sus vértices:
![]()
b) Calcule el máximo de la función ![]() en el recinto anterior e indique dónde se alcanza.
en el recinto anterior e indique dónde se alcanza.
Resuelve gráficamente el siguiente sistema de inecuaciones y calcula los vértices del recinto solución:
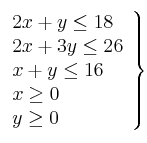
Un comerciante dispone de ![]() de piel de armiño,
de piel de armiño, ![]() de piel de zorro y
de piel de zorro y ![]() de cuero. Fabrica dos tipos de abrigos: A y B. Para los abrigos de tipo A usa
de cuero. Fabrica dos tipos de abrigos: A y B. Para los abrigos de tipo A usa ![]()
de piel de armiño, ![]() de piel de zorro y
de piel de zorro y ![]() de cuero. Para los abrigos de tipo B usa
de cuero. Para los abrigos de tipo B usa ![]() de piel de armiño,
de piel de armiño, ![]() de piel de zorro y
de piel de zorro y ![]() de cuero. Los abrigos de tipo A los vende a 800€ y los de tipo B a 1900€. ¿cuántos abrigos tiene que fabricar de cada tipo para obtener unos ingresos máximos?
de cuero. Los abrigos de tipo A los vende a 800€ y los de tipo B a 1900€. ¿cuántos abrigos tiene que fabricar de cada tipo para obtener unos ingresos máximos?
Un orfebre fabrica dos tipos de joyas. Las de tipo A precisan 1 gramo de oro y 1,5 gramos de plata, vendiéndolas a 40 euros cada una. Para la fabricación de las del tipo B emplea 1,5 gramos de oro y 1 gramo de plata y las vende a 50 euros. El orfebre tiene sólo en el taller 750 gramos de oro y 750 gramos de plata. ¿Cuántas joyas ha de fabricar de cada clase para obtener un ingreso máximo?
Unos grandes almacenes desean liquidar 200 camisas y 100 pantalones de la temporada anterior. Para ello lanzan dos ofertas: A y B. La oferta A consiste en un lote de una camisa y un pantalón, que se vende a 30 euros. La oferta B consiste en un lote de 3 camisas y 1 pantalón y se vende a 50 euros. No se desea ofrecer menos de 20 lotes de la oferta A, ni menos de 10 lotes de la oferta B. ¿Cuántos lotes ha de vender de cada tipo para maximizar las ganancias?
Se desea fabricar dos tipos de cajas de bombones que llamaremos A y B. Las cajas de tipo A contienen 1 kg de chocolate y 2 kg de cacao; las de tipo B contienen 2 kg de chocolate, 1 kg de cacao y 1 kg de almendras. Por cada caja del tipo A se ganan 2 € y por cada caja del tipo B, 3 €. Se dispone de 500 kg de chocolate, 400 kg de cacao y 225 kg de almendras.
¿Cuántas cajas de cada tipo hay que fabricar para que la ganancia sea máxima?
¿A cuánto asciende esta ganancia máxima?
Cierta compañía produce dos tipos de alimentos para perros, marcas A y B, respectivamente. Cada lata de la marca A contiene 200 g de carne y 100 g de harina. La marca B contiene 140 g de carne y 160 g de harina por lata.
Las instalaciones pueden manipular un máximo de 78 kg. de carne y 48 kg. de harina por hora. Si el beneficio obtenido de la marca A es de 300 u.m. (unidades monetarias) por lata y el de la marca B es de 240 u.m. por lata, ¿Cuántas latas de cada marca deben producirse por hora para maximizar el beneficio?
Averigua cómo se alcanzará el beneficio máximo.
Un pastor suministra a sus ovejas dos tipos de pienso con un contenido vitamínico por kilo como muestra la siguiente tabla. Ha de suministrarle diariamente al menos 5 mg de la vitamina A1 y 7 mg de la vitamina A2.
| A1 | A2 | |
| Pienso tipo 1 | 3 | 5 |
| Pienso tipo 2 | 4 | 2 |
El precio del kilo de pienso del tipo 1 es de 0’5 euros, y el kilo de pienso del tipo 2 de 0’7 euros.
Si asignamos “x” al número de kilos de pienso de tipo 1 e “y” al número de kilos del pienso de tipo 2 que han de mezclarse para tener un coste mínimo, escribe las restricciones propias de este problema así como la función objetivo.
Dadas las siguientes restricciones:
![]()
![]()
![]()
![]()
Encuentra en qué punto de la región limitada por las inecuaciones anteriores se hace máximo la función ![]()
 Matemáticas IES
Matemáticas IES