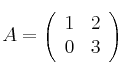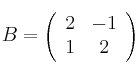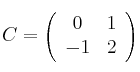EJERCICIOS RESUELTOS - Matrices, Determinantes y Sistemas
Matrices, Determinantes y Sistemas de Ecuaciones - 2º Bach. Sociales
Averigua las dimensiones de las matrices ![]() ,
, ![]() y
y ![]() para que se cumplan todas las condiciones siguientes:
para que se cumplan todas las condiciones siguientes:
a) Se pueda sumar ![]() con una matriz
con una matriz ![]()
b) Se pueda multiplicar ![]() pero no
pero no ![]()
c) Se pueda calcular ![]()
d) ![]() tenga el mismo número de columnas que
tenga el mismo número de columnas que ![]() de filas.
de filas.
e) El rango de ![]() es
es ![]() y coincide con su número de columnas.
y coincide con su número de columnas.
Sea la matriz 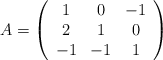
Justifica por qué existe la inversa y calcúlala.
Sean las matrices 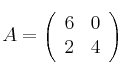 ,
, 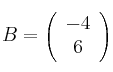 ,
, ![]()
a) Justifique cuáles de las siguientes operaciones se pueden realizar y efectúelas
cuando sea posible:
![]()
![]()
b) Resuelva la siguiente ecuación matricial: 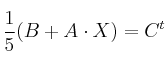
Calcula la inversa de la siguiente matriz usando el método de Gauss-Jordan
![]()
Dada la siguiente tabla
| Arroz 1 kg | Patatas 1 kg | Tomates 1 kg | |
|---|---|---|---|
| Supermercado 1 | 1.25 euros | 0.8 euros | 1.15 euros |
| Supermercado 2 | 1.5 euros | 75 céntimos | 1.2 euros |
| Supermercado 3 | 1.35 euros | 0.9 euros | 1 euros y 30 céntimos |
a) Expresa los datos mediante una matriz que llamaremos A.
b) ¿Es una matriz cuadrada? Justifica tu respuesta. Escribe la dimensión de la matriz.
c) Identifica en la matriz el elemento ![]() . ¿A qué elemento de la matriz correspondería el valor 1,15 euros?
. ¿A qué elemento de la matriz correspondería el valor 1,15 euros?
d) Escribe los valores de la diagonal principal y a qué elementos de la matriz corresponderían.
e) Escribe la matriz ![]() (traspuesta de A).
(traspuesta de A).
Dada la matriz
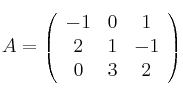
a) Calcula |A| (determinante de A)
b) Calcula el rango de A por determinantes o por Gauss.
Dadas las matrices
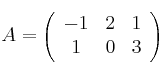 ,
, ![]() ,
, 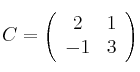 ,
, 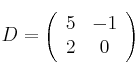
De las operaciones siguientes, indica justificadamente cuáles no se pueden realizar y efectúa todas aquellas que puedas hacer.
a) ![]()
b) ![]()
c) ![]()
d) ![]()
e) ![]()
Sean las matrices
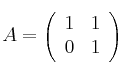
![]()
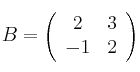
– Resuelve la ecuación matricial ![]()
– Calcule ![]()
Sean las matrices A = 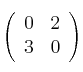 y B =
y B = 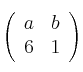
– a) Calcule los valores de a y b para que ![]()
– b) Para ![]() y
y ![]() , resuelva la ecuación matricial
, resuelva la ecuación matricial ![]()