-
Desde dos almacenes A y B, se tiene que distribuir fruta a tres mercados de la ciudad. El almacén A dispone de 10 toneladas de fruta diarias y el B de 15 toneladas, que se reparten en su totalidad. Los dos primeros mercados necesitan, diariamente, 8 toneladas de fruta, mientras que el tercero necesita 9 toneladas diarias.
El coste del transporte desde cada almacén a cada mercado viene dado por el siguiente cuadro:
PIZARRA
Planificar el transporte para que el coste sea mínimo.
-
Sean las matrices
a) Efectúe, si es posible, los siguientes productos:
– a1)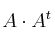 
– a2)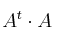 
– a3)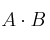 
b) Resuelva la siguiente ecuación matricial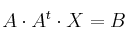 
-
Se considera el recinto R del plano, determinado por las siguientes inecuaciones:
, 
, 
, 
, 
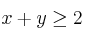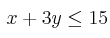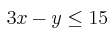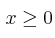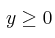
– (a) Represente gráficamente el recinto R y calcule sus vértices
– (b) Halle los valores máximo y mínimo que alcanza la función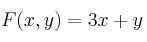 
en dicho recinto
– (c) Razone si existen puntos (x,y) del recinto, para los que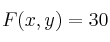 
-
Un cajero tiene 188 billetes que suponen un importe total de 7360 euros. Sabiendo que sólo dispone de dos tipos de billetes (de 50 euros y de 20 euros), plantea y resuelve un sistema de ecuaciones que te permita averiguar cuántos billetes tiene de cada tipo
-
Sean las matrices
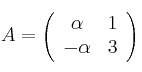
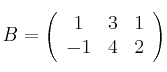
– a) Calcula los valores de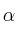 
para los que la matriz inversa de A es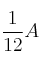 
– b) Para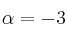 
, determina la matriz 
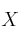que verifica la ecuación 
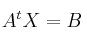, siendo 
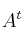la matriz traspuesta de 
.
PIZARRA
Matemáticas IES
