-
De los sucesos aleatorios 
y 
del mismo espacio de sucesos se sabe que:
, 
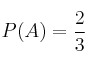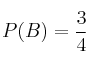y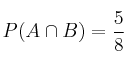 
. Calcule:
– a) La probabilidad de que se verifique alguno de los dos sucesos.
– b) La probabilidad de que no ocurra ninguno de los dos sucesos.
– c) La probabilidad de que ocurra si se ha verificado .
-
En cierto curso de un centro de enseñanza el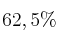 
de los alumnos aprobaron Matemáticas. por otro lado, entre quienes aprobaron Matemáticas el 
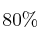aprobó también Física. Se sabe igualmente que sólo el 
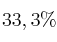de quienes no aprobaron Matemáticas, aprobaron Física. Se pide razonadamente:
– a) ¿Qué porcentaje consiguió aprobar ambas asignaturas?
– b) ¿Cuál es el porcentaje de aprobados en la asignatura de Física?
– c) Si un estudiante no aprobó Física, ¿qué probabilidad hay de que aprobara Matemáticas?
-
Una cadena metálica está compuesta por 4 eslabones. La probabilidad de rotura de cada eslabón a un peso de 100 kilos es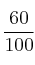 
. Se somete la cadena a un peso de 100 kilos, se pide de forma razonada:
– a) La probabilidad de que no se rompa la cadena
– b) Si se quiere que la probabilidad de que no se rompa la cadena sea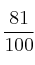 
, ?cuál debe ser la probabilidad de rotura de cada eslabón?
-
Se lanzan 3 monedas, la primera de 50 céntimos, la segunda de 1 euro y la tercera de 2 euros. Se consideran los sucesos: Suceso A aparecen dos caras, suceso B aparece una cara en la moneda de 2 euros y el suceso C aparecen caras en las monedas de 50 céntimos y de un euro. Se pide de forma razonada:
– a)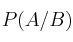 
– b) ¿Son independientes los sucesos B y C?
-
En un colegio hay 120 alumnos que cursan el bachillerato, 80 de ellos son de primero. Del total hay 64 chicas y 45 son chicas de primero. Elegimos un alumno al azar, se pide de forma razonada:
– a) ¿Cuál es la probabilidad de que el alumno elegido sea chico de segundo?.
– b) Si el alumno elegido se sabe que es de primero, ¿cuál es la probabilidad de que sea chica
Matemáticas IES
probabilidad
probabilidad