-
Sea la función 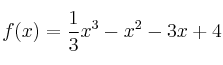
– a) Encuentre los puntos críticos de 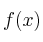 por medio del criterio de la primera derivada
por medio del criterio de la primera derivada
– b) Halle los intervalos donde la función es creciente y decreciente, así como los puntos máximos y mínimos
– c) Determine los puntos de inflexión
– d) Trace la gráfica de la función 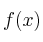
-
Sea la función:
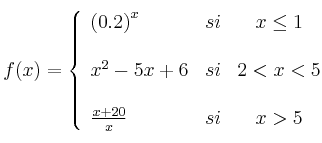
– a) Representación gráfica
– b) Indica Dominio, Corte con los ejes, Asíntotas, Monotonía y Extremos
-
Dada la función 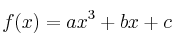 , determinar los valores de
, determinar los valores de  ,
, 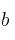 y
y 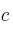 si sabemos que
si sabemos que  tiene un óptimo en
tiene un óptimo en 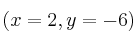 y la pendiente de la recta tangente a
y la pendiente de la recta tangente a  en
en 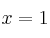 es
es 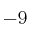 .
.
-
– a) Calcule la ecuación de la recta tangente a 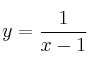 en el punto de abcisa
en el punto de abcisa 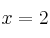
– b) ¿En qué punto de la gráfica de la función 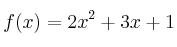 , la recta tangente es paralela a
, la recta tangente es paralela a 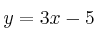 ?
?
– c) Sea 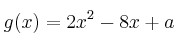 . Halle
. Halle  para que el valor mínimo de
para que el valor mínimo de 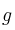 sea
sea 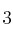
-
Se sabe que la función 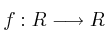 definida por
definida por
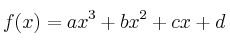
tiene extremos relativos en (0,0) y en (2,2). Calcula a,b,c,d
 extremos
extremos asíntotas
asíntotas bolzano
bolzano composición
composición continuidad
continuidad coordenadas
coordenadas corte_ejes
corte_ejes curvatura
curvatura definición de función
definición de función derivada de una función
derivada de una función dominio
dominio ecuacion_recta
ecuacion_recta estudio global de función
estudio global de función extremos
extremos función valor absoluto
función valor absoluto funciones
funciones funciones a trozos
funciones a trozos función_inversa
función_inversa gráfica
gráfica gráfica de logarítmica
gráfica de logarítmica gráfica_de_exponencial
gráfica_de_exponencial Matemáticas IES
Matemáticas IES
 extremos
extremos