-
Sea 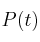 el porcentaje de células, de un determinado tejido, afectadas por un cierto tipo de enfermedad transcurrido un tiempo
el porcentaje de células, de un determinado tejido, afectadas por un cierto tipo de enfermedad transcurrido un tiempo 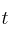 , medido en meses:
, medido en meses:
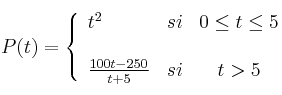
– a) Estudie la continuidad de la función P.
– b) Estudie la derivabilidad de P en 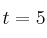 .
.
– c) Estudie la monotonía de dicha función e interprete la evolución del porcentaje de células afectadas.
– d) ¿En algún momento el porcentaje de células afectadas podría valer 50?
-
Se considera la función 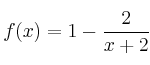
– a) Determine la monotonía y curvatura de la función.
– b) Calcule sus asíntotas.
– c) Represéntela gráficamente.
-
Se ha impartido un curso de “conducción eficiente” a 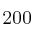 personas. De los asistentes al curso,
personas. De los asistentes al curso, 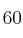 son profesores de autoescuela y, de ellos, el
son profesores de autoescuela y, de ellos, el 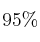 han mejorado su conducción. Este porcentaje baja al
han mejorado su conducción. Este porcentaje baja al 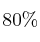 en el resto de los asistentes. Halle la probabilidad de que, elegido un asistente al azar:
en el resto de los asistentes. Halle la probabilidad de que, elegido un asistente al azar:
– a) No haya mejorado su conducción.
– b) No sea profesor de autoescuela, sabiendo que ha mejorado su conducción.
-
En una localidad hay solamente dos supermercados  y
y  . El
. El 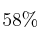 de los habitantes compra en el
de los habitantes compra en el  , el
, el 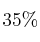 en el
en el  y el
y el 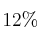 compra en ambos. Si se elige un ciudadano al azar, calcule la probabilidad de que:
compra en ambos. Si se elige un ciudadano al azar, calcule la probabilidad de que:
– a) Compre en algún supermercado.
– b) No compre en ningún supermercado.
– c) Compre solamente en un supermercado.
– d) Compre en el supermercado A, sabiendo que no compra en B.
-
Una compañía de seguros ha hecho un seguimiento durante un año a 50000 coches de la marca A, a 20000 de la marca B y a 30000 de la C, que tenía asegurados, obteniendo que, de ellos, habían tenido accidente 650 coches de la marca A, 200 de la B y 150 de la C. A la vista de estos datos:
– a) ¿Cuál de las tres marcas de coches tiene menos proporción de accidentes?
– b) Si, elegido al azar uno de los coches observados, ha tenido un accidente, ¿cuál es la probabilidad de que sea de la marca C?
 selectividad
selectividad andalucía
andalucía aragón
aragón asturias
asturias cantabria
cantabria castilla_leon
castilla_leon castilla_mancha
castilla_mancha catalunya
catalunya madrid
madrid MatemáticasII_Andalucía_2001
MatemáticasII_Andalucía_2001 MatemáticasII_Andalucía_2002
MatemáticasII_Andalucía_2002 MatemáticasII_Andalucía_2003
MatemáticasII_Andalucía_2003 MatemáticasII_Andalucía_2004
MatemáticasII_Andalucía_2004 MatemáticasII_Andalucía_2005
MatemáticasII_Andalucía_2005 MatemáticasII_Andalucía_2006
MatemáticasII_Andalucía_2006 MatemáticasII_Andalucía_2007
MatemáticasII_Andalucía_2007 MatemáticasII_Andalucía_2008
MatemáticasII_Andalucía_2008 MatemáticasII_Andalucía_2009
MatemáticasII_Andalucía_2009 MatemáticasII_Andalucía_2010
MatemáticasII_Andalucía_2010 MatematicasII_Andalucía_2011
MatematicasII_Andalucía_2011 MatemáticasII_Andalucía_2012
MatemáticasII_Andalucía_2012 Matemáticas IES
Matemáticas IES
 selectividad
selectividad