-
Los expertos en mercadeo de una compañía de artículos de aseo estiman que en el evento de lanzamiento de una marca, la probabilidad de que uno de los asistentes compre un detergente es 77%, la probabilidad de que compre un blanqueador es 85% y la probabilidad de que compre los dos artículos es 65%. A un asistente que compre únicamente uno de los dos productos se le obsequia un cepillo, y a los que compren los dos, un suavizante.
¿Cuántos cepillos se espera entregar en un evento al que asisten 450 personas?
-
En una clase con 15 alumnos y 15 alumnas hacen este experimento:
Tienen una urna A con 10 bolas numeradas de 1 a 10 y una urna B con 5 bolas numeradas de 1 a 5, eligen al azar una persona de la clase, si es alumna, saca una bola de la urna A, y si es un chico, saca una bola de la urna B.
a) ¿Cuál es la probabilidad de sacar un número par?
b) Si ha salido un número par, ¿cuál es la probabilidad de que lo haya sacado una chica?
-
En el instituto, el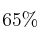 
de las personas son alumnos/as, el 
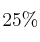profesores y el 
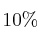personal no docente. Son mujeres el 
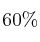del alumnado, el 
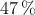del profesorado y el 
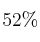del personal no docente. Si seleccionamos al azar una persona del instituto:
a) Calcula la probabilidad de que sea mujer.
b) Sabiendo que la persona seleccionada ha resultado ser hombre, hallar la probabilidad de que sea alumno.
-
En la localidad almeriense de Pulpí el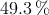 
de los habitantes son hombres, de los cuales el 
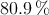tienen menos de 65 años. Hay un 
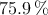de mujeres con menos de 65 años.
a) Elegimos un habitante al azar. Calcula la probabilidad de que sea una mujer de menos de 65 años
b) Elegimos un habitante al azar. Calcula la probabilidad de que tenga menos de 65 años
c) Elegimos un habitante al azar de entre los que tienen menos de 65 años. Calcula la probabilidad de que sea mujer
d) Elegimos tres habitantes al azar (con reemplazamiento). Calcula la probabilidad de que al menos uno de los tres sea mujer.
-
Un juego consiste en hacer dos lanzamientos a portería vacía desde 70 metros. La probabilidad de acertar es 0.3 en cada lanzamiento. Ganas el premio si aciertas en alguno de los dos lanzamientos. Calcula:
a) Probabilidad de acertar los dos lanzamientos
b) Probabilidad de ganar el premio.
c) Sabiendo que ganamos el premio, ¿Qué probabilidad hay de haber fallado el primer lanzamiento?
d) Si A es el suceso "Fallar el primer lanzamiento" y B es "Ganar el premio", ¿Son independientes los sucesos A y B?
Matemáticas IES
probabilidad
probabilidad