-
En el mar hay una mancha producida por una erupción marina. La superficie afectada, en 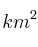 , viene dada por la función
, viene dada por la función 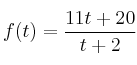 , siendo
, siendo 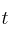 el tiempo transcurrido desde que empezamos a observarla.
el tiempo transcurrido desde que empezamos a observarla.
– a) ¿Cuál es la superficie afectada inicialmente, cuando empezamos a medirla?
– b) Estudie si la mancha crece o decrece con el tiempo
– c) ¿Tiene algún límite la extensión de la superficie de la mancha?
-
El gerente de una empresa sabe que los beneficios de la misma, 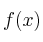 , dependen de la inversión,
, dependen de la inversión, 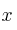 , según la función
, según la función 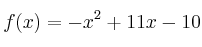 . (x es la cantidad invertida en millones de euros).
. (x es la cantidad invertida en millones de euros).
– a) Determine los valores de la inversión para los que la función beneficio es no negativa.
– b) Halle el valor de la inversión para el cual el beneficio es máximo. ¿A cuánto asciende éste?
– c) ¿Entre qué valores ha de estar comprendida la inversión para que el beneficio sea creciente, sabiendo que éste es no negativo?
-
Sea la función 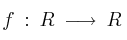 definida por
definida por 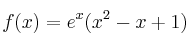
– a) Calcula 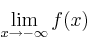 y
y 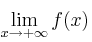
– b) Halla los extremos relativos de f (abscisas donde se obtienen y valores que se alcanzan), determinando si son máximos o mínimos.
– c) Determina las abscisas de los puntos de inflexión de la gráfica de  .
.
-
Se consideran dos sucesos  y
y  asociados a un experimento aleatorio. Se sabe que
asociados a un experimento aleatorio. Se sabe que 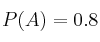 ,
, 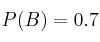 y
y 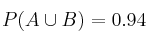
– a) ¿Son  y
y  sucesos independientes?
sucesos independientes?
– b) Calcule 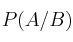
– c) Calcule 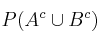
-
Una urna contiene 25 bolas blancas sin marcar, 75 bolas blancas marcadas, 125 bolas negras sin marcar y 175 bolas negras marcadas. Se extrae una bola al azar.
– a) Calcule la probabilidad de que sea blanca.
– b) ¿Cuál es la probabilidad de que sea blanca sabiendo que está marcada?
– c) ¿Cuál es la probabilidad de que sea negra y esté marcada?
– d) ¿Son independientes los sucesos "sacar bola marcada" y "sacar bola blanca"?
 selectividad
selectividad andalucía
andalucía aragón
aragón asturias
asturias cantabria
cantabria castilla_leon
castilla_leon castilla_mancha
castilla_mancha catalunya
catalunya madrid
madrid MatemáticasII_Andalucía_2001
MatemáticasII_Andalucía_2001 MatemáticasII_Andalucía_2002
MatemáticasII_Andalucía_2002 MatemáticasII_Andalucía_2003
MatemáticasII_Andalucía_2003 MatemáticasII_Andalucía_2004
MatemáticasII_Andalucía_2004 MatemáticasII_Andalucía_2005
MatemáticasII_Andalucía_2005 MatemáticasII_Andalucía_2006
MatemáticasII_Andalucía_2006 MatemáticasII_Andalucía_2007
MatemáticasII_Andalucía_2007 MatemáticasII_Andalucía_2008
MatemáticasII_Andalucía_2008 MatemáticasII_Andalucía_2009
MatemáticasII_Andalucía_2009 MatemáticasII_Andalucía_2010
MatemáticasII_Andalucía_2010 MatematicasII_Andalucía_2011
MatematicasII_Andalucía_2011 MatemáticasII_Andalucía_2012
MatemáticasII_Andalucía_2012 Matemáticas IES
Matemáticas IES
 selectividad
selectividad