-
Sea la función 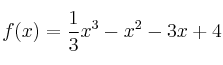
– a) Encuentre los puntos críticos de 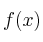 por medio del criterio de la primera derivada
por medio del criterio de la primera derivada
– b) Halle los intervalos donde la función es creciente y decreciente, así como los puntos máximos y mínimos
– c) Determine los puntos de inflexión
– d) Trace la gráfica de la función 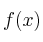
-
Un industrial desea construir una caja abierta, es decir sin tapa, de base cuadrada y superficie total 108 centímetros cuadrados. ¿Qué dimensiones tendrá la caja de volumen máximo?
-
Un granjero quiere bordear un área de 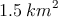 en un campo rectangular y luego dividirlo a la mitad con una barda paralela a un lado del rectángulo. ¿Cómo puede hacerlo para minimizar el costo de la barda?
en un campo rectangular y luego dividirlo a la mitad con una barda paralela a un lado del rectángulo. ¿Cómo puede hacerlo para minimizar el costo de la barda?
-
Un trozo de alambre de 10 metros de largo se corta en dos partes. Una se dobla para formar un cuadrado y la otra para formar un triángulo equilátero. Determine cómo debe cortarse el alambre de modo que el área total encerrada sea:
– a) Máxima
– b) Mínima
-
Represente gráficamente la función 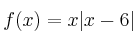
 funciones
funciones asíntotas
asíntotas bolzano
bolzano composición
composición continuidad
continuidad coordenadas
coordenadas corte_ejes
corte_ejes curvatura
curvatura definición de función
definición de función derivada de una función
derivada de una función dominio
dominio ecuacion_recta
ecuacion_recta estudio global de función
estudio global de función extremos
extremos función valor absoluto
función valor absoluto funciones
funciones funciones a trozos
funciones a trozos función_inversa
función_inversa gráfica
gráfica gráfica de logarítmica
gráfica de logarítmica gráfica_de_exponencial
gráfica_de_exponencial Matemáticas IES
Matemáticas IES
 funciones
funciones