-
A continuación puedes ver la gráfica de una función definida a trozos. Obtén la expresión analítica, utilizando las expresiones adecuadas.
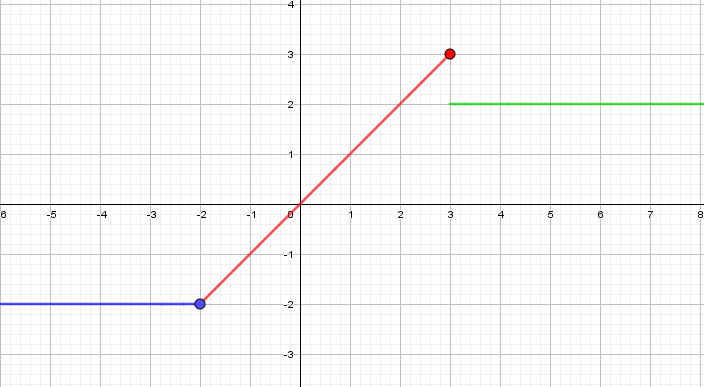
gráfica
-
En la siguiente función indica:
a) Dominio
b) Recorrido
c) Extremos relativos (máximos y mínimos)
d) Puntos de corte. Si no coincide con un valor entero, utiliza una cifra decimal para expresarlo.
e) Monotonía (intervalos de crecimiento y decrecimiento)
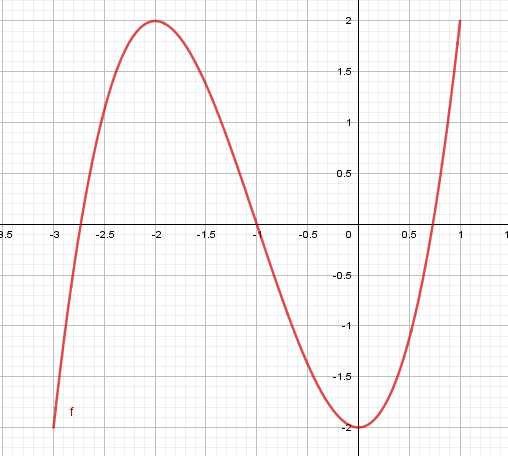
gráfica
-
Dadas las siguientes funciones, definidas por su expresión algebraica, selecciona la gráfica que corresponde a cada una e indica de qué tipo de función se trata.
a)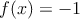 
b)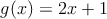 
c)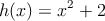 
gráfica
-
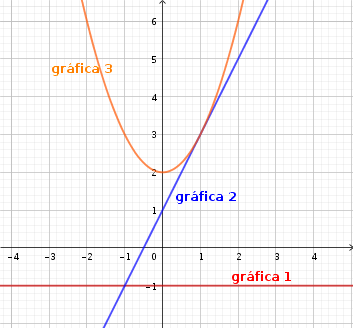
Una pelotita se coloca en la punta de una canal lisa y comienza a rodar por ella. La figura muestra cómo varía la altura de la pelotita durante el recorrido por la canal hasta llegar al suelo
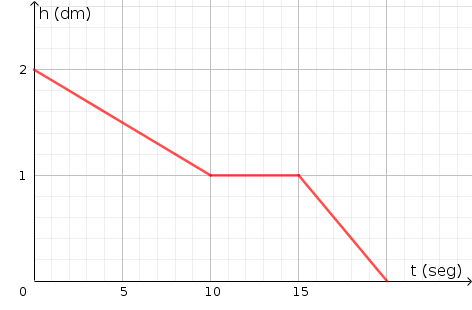
gráfica
a) ¿A qué altura se colocó inicialmente la pelotita?
b) ¿En qué intervalo de tiempo la altura de la pelota no varió?
c) Determina mediante cálculos a qué altura estaba la pelota a los 4 segundos.
d) Si la ecuación que describe el descenso de la pelota después de los 15 segundos es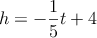 
, ¿Cuánto tiempo tardó en llegar al suelo?
e) ¿En cuál de los dos tramos de descenso, la pelota rodó más rápido?. Argumenta tu respuesta
-
Dada la siguiente función:
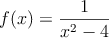
Haz un estudio completo de la misma siguiendo los siguientes pasos:
a) Halla el dominio de la función.
b) Haz un estudio de las simetrías que presenta (si es par, impar o ninguna de las dos cosas).
c) Halla los puntos de corte con los ejes.
d) Haz un estudio de las asíntotas que presenta (verticales, horizontales y oblicuas).
e) Haz un estudio de la monotonía (crecimiento y decrecimiento) y de los extremos que presenta (máximos y mínimos).
f) Haz un estudio de la curvatura (concavidad y convexidad) y de los puntos de inflexión.
g) Representa gráficamente la función con Geogebra
Matemáticas IES
gráfica
gráfica