-
El consumo de cereales en una ciudad, en miles de toneladas, viene dado por la función 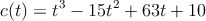 , para
, para 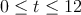 , donde
, donde 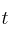 representa el tiempo.
representa el tiempo.
– a) ¿En qué instante se alcanza el máximo consumo de cereales y cuántas toneladas se consumen en ese momento?
– b) ¿En qué intervalo de tiempo decrece el consumo de cereales?
– c) Represente gráficamente la función.
-
Para la función 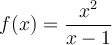 , se pide:
, se pide:
a) Dominio de definición y puntos de corte con los ejes.
b) Estudio de las asíntotas (verticales, horizontales y oblicuas).
c) Intervalos de crecimiento y decrecimiento. Extremos (máximos y mínimos).
d) Representación gráfica aproximada.
-
Dada la función 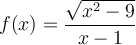 , se pide:
, se pide:
a) Dominio de definición y puntos de corte con los ejes.
b) Estudio de las asíntotas (verticales, horizontales y oblicuas).
c) Intervalos de crecimiento y decrecimiento. Extremos (máximos y mínimos).
d) Representación gráfica aproximada.
-
Dada la función 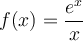 , se pide:
, se pide:
a) Dominio de definición y cortes con los ejes.
b) Estudio de las asíntotas (verticales, horizontales y oblicuas).
c) Intervalos de crecimiento y decrecimiento. Extremos (máximos y mínimos).
d) Representación gráfica aproximada.
-
Estudia monotonía y extremos en la función 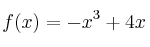
 extremos
extremos asíntotas
asíntotas bolzano
bolzano composición
composición continuidad
continuidad coordenadas
coordenadas corte_ejes
corte_ejes curvatura
curvatura definición de función
definición de función derivada de una función
derivada de una función dominio
dominio ecuacion_recta
ecuacion_recta estudio global de función
estudio global de función extremos
extremos función valor absoluto
función valor absoluto funciones
funciones funciones a trozos
funciones a trozos función_inversa
función_inversa gráfica
gráfica gráfica de logarítmica
gráfica de logarítmica gráfica_de_exponencial
gráfica_de_exponencial Matemáticas IES
Matemáticas IES
 extremos
extremos