-
a) Plantee, sin resolver, las restricciones de este problema e indique la función a optimizar:
"Un ganadero alimenta a sus ovejas con maíz y pienso. Cada kilogramo de maíz aporta 600 g de hidratos de carbono y 200 g de proteínas, mientras que cada kilogramo de pienso aporta 300 g de hidratos de carbono y 600 g de proteínas. Cada oveja necesita diariamente como mínimo 1800 g de hidratos de carbono y 2400 g de proteínas. Si 1 kg de maíz cuesta 0.50 euros y 1 kg de pienso cuesta 0.25 euros, calcule cuántos kilogramos de cada producto tendría que comprar el ganadero para alimentar cada día a una oveja con un gasto mínimo".
b) Represente el recinto limitado por las siguientes restricciones, calculando sus vértices
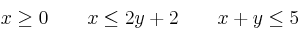
Calcule el máximo de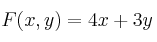 
en ese recinto, así como el punto donde se alcanza
.
-
Un pastor suministra a sus ovejas dos tipos de pienso con un contenido vitamínico por kilo como muestra la siguiente tabla. Ha de suministrarle diariamente al menos 5 mg de la vitamina A1 y 7 mg de la vitamina A2.
|
A1 |
A2 |
| Pienso tipo 1 |
3 |
5 |
| Pienso tipo 2 |
4 |
2 |
El precio del kilo de pienso del tipo 1 es de 0’5 euros, y el kilo de pienso del tipo 2 de 0’7 euros.
Si asignamos “x” al número de kilos de pienso de tipo 1 e “y” al número de kilos del pienso de tipo 2 que han de mezclarse para tener un coste mínimo, escribe las restricciones propias de este problema así como la función objetivo.
-
Dadas las siguientes restricciones:
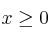
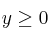
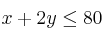
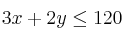
Encuentra en qué punto de la región limitada por las inecuaciones anteriores se hace máximo la función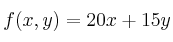 
-
Un fabricante diseña pantalones y camisas. Para ello dispone de 50 metros de tejido de algodón y 124 metros de tejido de lino. Cada pantalón precisa 0.75 metros de algodón y 2 metros de lino. Para cada camisa se necesitan 0.5 metros de algodón y 1 metro de lino. El precio de mercado del pantalón es de 40 euros y el de la camisa de 25 euros. Se trata de encontrar el número de pantalones y camisas que debe diseñar el fabricante para obtener unos ingresos máximos.
-
Se quiere organizar un puente aéreo entre dos ciudades, con plazas suficientes de pasaje y carga, para transportar 1600 personas y 96 toneladas de equipaje. Los aviones disponibles son de dos tipos: 11 del tipo A y 8 del tipo B. La contratación de un avión del tipo A cuesta 4 millones de pts y puede transportar 200 personas y 6 toneladas de equipaje; la contratación de uno del tipo B cuesta 1 millón de pts y puede transportar 100 personas y 15 toneladas de equipaje.
¿Cuántos aviones de cada tipo deben utilizarse para que el coste sea mínimo?.
Matemáticas IES
programación_lineal