-
Conjunto de exámenes de Selectividad de la asignatura:
Matemáticas Aplicadas a las Ciencias Sociales II
en la comunidad de Andalucía.
Exámenes del año 2011
También le puede interesar:
– Ejercicios Resueltos de Selectividad Andalucía
-
El director de un banco afirma que la cantidad media de dinero extraído, por cliente, de un cajero automático de su sucursal no supera los 120 euros. Para contrastar esta hipótesis elige al azar 100 extracciones de este cajero y obtiene una media muestral de 130 euros. Se sabe que la cantidad de dinero extraído por un cliente en un cajero automático se distribuye según una ley Normal de media desconocida y desviación típica 67 euros.
– a) Plantee el contraste de hipótesis asociado al enunciado.
– b) Determine la región de aceptación, para un nivel de significación α =0.05.
– c) Con los datos muestrales tomados, ¿existe evidencia estadística para rechazar la hipótesis de este director, con el mismo nivel de significación anterior?
-
Una máquina de envasado está diseñada para llenar bolsas con 300 g de almendras. Para comprobar si funciona correctamente, se toma una muestra de 100 bolsas y se observa que su peso medio es de 297 g. Suponiendo que la variable “peso” tiene una distribución Normal con varianza 16, y utilizando un contraste bilateral ¿es aceptable, a un nivel de significación de 0.05, que el funcionamiento de la máquina es correcto?
-
Un banco lanza al mercado un plan de inversión cuya rentabilidad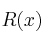 
, en miles de euros, viene dada en función de la cantidad, 
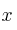, que se invierte, también en miles de euros, por la siguiente expresión:
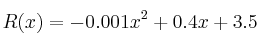, con 
.
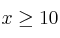– a) Calcule la rentabilidad para una inversión de 100000 euros.
– b) Deduzca y razone qué cantidad habría que invertir para obtener la máxima rentabilidad.
– c) ¿Qué rentabilidad máxima se obtendría?
-
Tras un test realizado a un nuevo modelo de automóvil, se ha observado que el consumo de gasolina,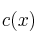 
, expresado en litros, viene dado por la función
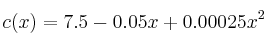
siendo 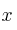, la velocidad en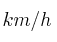 
– a) Determine el consumo de gasolina a las velocidades de 50 km/h y 150 km/h.
– b) Estudie el crecimiento y decrecimiento de la función c(x) .
– c) ¿A qué velocidades de ese intervalo se obtiene el mínimo consumo y el máximo consumo y cuáles son éstos?
Matemáticas IES
selectividad
selectividad