-
Sea 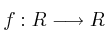 la función definida por
la función definida por 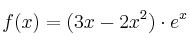
– (a) Determina los intervalos de crecimiento y de decrecimiento de 
– (b) Calcula los extremos relativos de  (abcisas donde se obtienen y valores que se alcanzan)
(abcisas donde se obtienen y valores que se alcanzan)
-
Sea la función 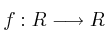 definida por:
definida por:
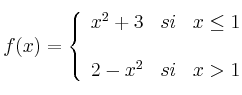
– (a) Calcula, si es posible, las derivadas laterales de  en
en 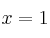
– (b) Halla los intervalos de crecimiento y de decrecimiento de la función 
-
Sea la función 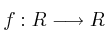 definida por:
definida por:
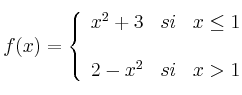
– (a) Calcula, si es posible, las derivadas laterales de  en
en 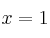
– (b) Halla los intervalos de crecimiento y de decrecimiento de la función 
-
Sea  la función definida por
la función definida por 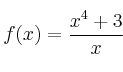 , para
, para 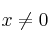 .
.
– (a) Halla, si existen, los puntos de corte con los ejes y las asíntotas de la gráfica de  .
.
– (b) Calcula los intervalos de crecimiento y decrecimiento y los extremos relativos de  .
.
– (c) Esboza la gráfica de  .
.
-
Realiza un estudio global (dominio, simetrías, corte con los ejes, asíntotas, monotonía, extremos y representación gráfica) de la función:
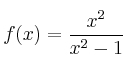
 monotonía
monotonía asíntotas
asíntotas bolzano
bolzano composición
composición continuidad
continuidad coordenadas
coordenadas corte_ejes
corte_ejes curvatura
curvatura definición de función
definición de función derivada de una función
derivada de una función dominio
dominio ecuacion_recta
ecuacion_recta estudio global de función
estudio global de función extremos
extremos función valor absoluto
función valor absoluto funciones
funciones funciones a trozos
funciones a trozos función_inversa
función_inversa gráfica
gráfica gráfica de logarítmica
gráfica de logarítmica gráfica_de_exponencial
gráfica_de_exponencial Matemáticas IES
Matemáticas IES
 monotonía
monotonía