-
Sean  y
y  dos matrices cuadradas de orden 3 cuyos determinantes son
dos matrices cuadradas de orden 3 cuyos determinantes son 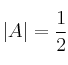 y
y 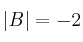 . Halla:
. Halla:
– a) 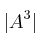
– b) 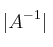
– c) 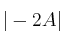
– d) 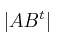
– e) rango(B)
-
Considera las matrices
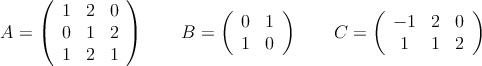
Determina, si existe, la matriz 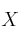 que verifica
que verifica 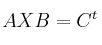 , siendo
, siendo 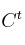 la matriz traspuesta de
la matriz traspuesta de 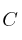
-
Dada la matriz
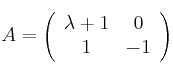
– a) Determina los valores de 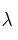 para los que la matriz
para los que la matriz 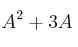 no tiene inversa.
no tiene inversa.
– b) Para 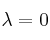 , halla la matriz
, halla la matriz 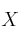 que verifica la ecuación
que verifica la ecuación 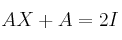 , siendo
, siendo 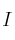 la matriz identidad de orden 2.
la matriz identidad de orden 2.
-
Considera las matrices:
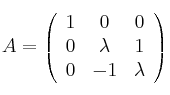
 y
y 
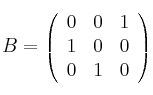
– a) ¿Hay algún valor de 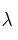 para el que
para el que  no tiene inversa?
no tiene inversa?
– b) Para 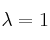 , resuelve la ecuación matricial
, resuelve la ecuación matricial 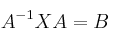
-
Sean las matrices:
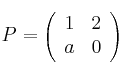 ,
,
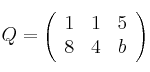 y
y
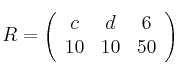
– a) Calcule, si es posible, 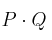 y
y 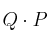 , razonando la respuesta
, razonando la respuesta
– b) ¿Cuánto deben valer las constantes a, b, c y d para que 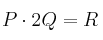 ?
?
 matrices
matrices