-
En una empresa de montajes el número de montajes diarios realizados por un trabajador depende de los días trabajados según la función
,
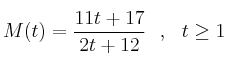donde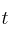 
es el número de días trabajados.
– a) ¿Cuántos montajes realiza el primer día? ¿Cuántos días necesitará para
realizar cinco montajes diarios?
– b) ¿Qué ocurriría con el número de montajes diarios si trabajara indefinidamente?
– c) El dueño de la empresa cree que el número de montajes diarios aumenta con los días de trabajo. Estudiando la función, justifique si es cierta dicha creencia.
– d) Dibuje la gráfica de la función.
-
En una urna A hay 10 bolas verdes y 10 rojas, y en otra urna B hay 15 verdes y 5 rojas. Se lanza un dado, de forma que si sale múltiplo de 3 se extrae una bola de la urna A y en el resto de casos se extrae una bola de la urna B.
– a) Calcule la probabilidad de que la bola extraída sea roja.
– b) Si la bola extraída resulta ser de color verde, ¿cuál es la probabilidad de que
proceda de la urna B?
-
En una empresa, el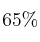 
de sus empleados habla inglés, y de éstos, el 
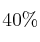habla también alemán. De los que no hablan inglés, el 
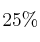habla alemán. Se escoge un empleado al azar:
– a) ¿Cuál es la probabilidad de que hable ambos idiomas?
– b) ¿Cuál es la probabilidad de que hable alemán?
– c) ¿Cuál es la probabilidad de que, sabiendo que habla alemán, hable
también inglés?
-
De los sucesos independientes 
y 
se sabe que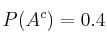 
y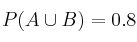 
– a) Halle la probabilidad de
– b) Halle la probabilidad de que no se verifique si se ha verificado
– c) ¿Son incompatibles los sucesos y ?
-
Una granja avícola dedicada a la producción de huevos posee un sistema automático de clasificación en tres calibres según su peso: grande, mediano y pequeño. Se conoce que el 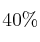de la producción es clasificada como huevos grandes, el 
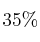como medianos y el 
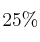restante como pequeños. Además, se sabe que este sistema de clasificación produce defectos por rotura en el cascarón que dependen del peso. Así, la probabilidad de que un huevo grande sea defectuoso por esta razón es del 
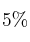, la de uno mediano del 
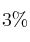y de un
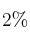la de uno pequeño. Elegido aleatoriamente un huevo,
– a) ¿cuál es la probabilidad de que sea defectuoso?
– b) Si el huevo es defectuoso, ¿cuál es la probabilidad de que sea grande?
Ejercicios_Resueltos
Matemáticas IES
