-
Se considera el recinto R del plano, determinado por las siguientes inecuaciones:
, 
, 
, 
, 
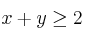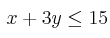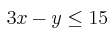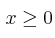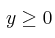
– (a) Represente gráficamente el recinto R y calcule sus vértices
– (b) Halle los valores máximo y mínimo que alcanza la función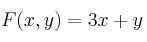 
en dicho recinto
– (c) Razone si existen puntos (x,y) del recinto, para los que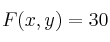 
-
Un cajero tiene 188 billetes que suponen un importe total de 7360 euros. Sabiendo que sólo dispone de dos tipos de billetes (de 50 euros y de 20 euros), plantea y resuelve un sistema de ecuaciones que te permita averiguar cuántos billetes tiene de cada tipo
-
Sean las matrices
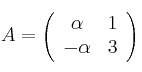
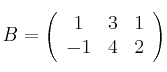
– a) Calcula los valores de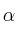 
para los que la matriz inversa de A es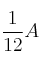 
– b) Para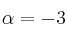 
, determina la matriz 
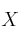que verifica la ecuación 
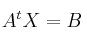, siendo 
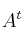la matriz traspuesta de 
.
-
Dadas las matrices
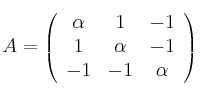
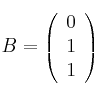
– a) Calcula el rango de dependiendo de los valores de
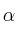
– b) Para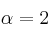 
, resuelve la ecuación matricial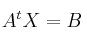
-
Sabemos que la fabricación de un envase tetra brik emite 62 gramos de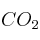 
y que conducir un coche durante 1 km emite 211 gramos de 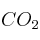. Plantea y resuelve una inecuación para saber cuántos tetra brik es necesario fabricar para superar el consumo de 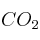producido por la conducción durante 50 km de un coche.
Ejercicios_Resueltos
Matemáticas IES
