-
Considera las matrices
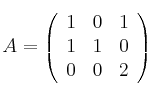 y
y
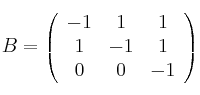
– (a) Halla, si es posible, 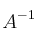 y
y 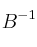
– (b) Halla el determinante de 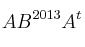 siendo
siendo 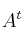 la matriz traspuesta de
la matriz traspuesta de 
– (c) Calcula la matriz 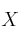 que satisface
que satisface 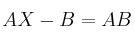
-
Sean las matrices
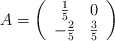
,
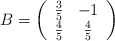
,
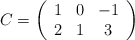
– a) Resuelva la ecuación matricial 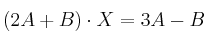
– b) Determine en cada caso la dimensión de la matriz D para que se puedan realizar las siguientes operaciones: 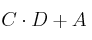 ,
, 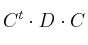 ,
, 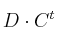 ,
, 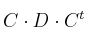
-
Sea 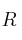 la región factible definida por las siguientes inecuaciones
la región factible definida por las siguientes inecuaciones 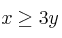 ,
, 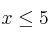 ,
, 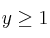 .
.
– a) (0.5 puntos) Razone si el punto 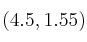 pertenece a
pertenece a 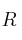 .
.
– b) (1.5 puntos) Dada la función objetivo 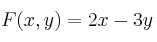 , calcule sus valores extremos en
, calcule sus valores extremos en 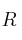 .
.
– c) (0.5 puntos) Razone si hay algún punto de 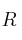 donde la función
donde la función 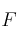 valga
valga 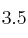 . ¿Y
. ¿Y 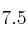 ?
?
-
Resuelve las siguientes ecuaciones:
– 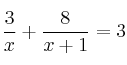
– 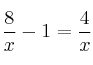
-
Sean  y
y  dos matrices cuadradas de orden 3 cuyos determinantes son
dos matrices cuadradas de orden 3 cuyos determinantes son 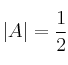 y
y 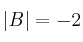 . Halla:
. Halla:
– a) 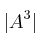
– b) 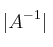
– c) 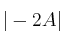
– d) 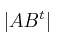
– e) rango(B)
 Ejercicios_Resueltos
Ejercicios_Resueltos