-
Dada la función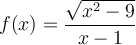 
, se pide:
a) Dominio de definición y puntos de corte con los ejes.
b) Estudio de las asíntotas (verticales, horizontales y oblicuas).
c) Intervalos de crecimiento y decrecimiento. Extremos (máximos y mínimos).
d) Representación gráfica aproximada.
-
Dada la función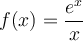 
, se pide:
a) Dominio de definición y cortes con los ejes.
b) Estudio de las asíntotas (verticales, horizontales y oblicuas).
c) Intervalos de crecimiento y decrecimiento. Extremos (máximos y mínimos).
d) Representación gráfica aproximada.
-
Considere la función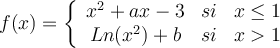 
Determine los valores de los parámetros 
y 
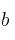para los cuales la función 
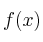es continua y derivable en todo R.
-
Un tanque de reserva de agua utiliza una bomba neumática para surtirse del río cercano. Todos los días la bomba sube el nivel del agua 0.5 m, pero por la noche, el agua se filtra de regreso al río y baja el nivel en un 35 por ciento de lo recolectado durante el día.
1- ¿Cuánto sube el nivel del agua en un día completo (en metros)?
2- ¿Cuánto subirá el nivel del agua en 6 días completos (en metros)?
3- ¿Cuál será el nivel máximo de agua alcanzado en el día 6 (en metros)?
-
Sean L1 y L2 las rectas de ecuación
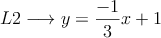
donde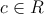 
a) Determinar el valor de c para el cual la recta L1 ea perpendicular a la recta L2. Escribir la ecuación de la recta L1
b) Hallar analíticamente el punto de intersección de las rectas L1 y L2 y verificar gráficamente el resultado hallado.
c) Encontrar la ecuación de la recta L que es paralela a la recta L1 y pasa por el punto P= ( -1/3 , 1/3)
Ejercicios_Resueltos
Matemáticas IES
