-
Encuentra dos puntos y dos vectores directores de las siguientes rectas:
a)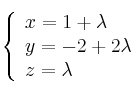 
b)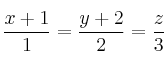 
c)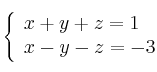 
-
Dados los puntos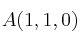 
y 
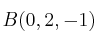, escriba las ecuaciones paramétricas, continua e implícitas de la recta que pasa por los puntos 
y 
-
Dados los vectores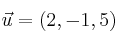 
, 
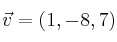y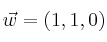 
, se pide:
– a) ¿Son linealmente dependientes los 3 vectores?
– b) Calula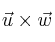 
(producto vectorial)
– c) Encuentra dos vectores paralelos al vector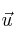 
– d) Encuentra dos vectores perpendiculares al vector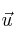
– e) Halla el ángulo que forman los vectores 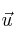y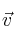 
-
Consideramos los puntos ,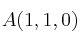 
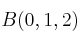y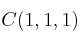 
.
– a) Calcula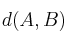 
(distancia entre los puntos A y B)
– b)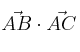 
(producto escalar)
– c) Calcula el perímetro del triángulo de vértices A, B y C
– d) Halla el área del triángulo de vértices A, B y C
-
Un Centro de Salud propone dos terapias, A y B, para dejar de fumar. De las personas que acuden al Centro para dejar de fumar, el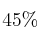 
elige la terapia A, y el resto la B. Después de un año el 
de los que siguieron la terapia A y el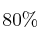 
de los que siguieron la B no han vuelto a fumar.
Se elige al azar un usuario del Centro que siguió una de las dos terapias:
– a) Calcule la probabilidad de que después de un año no haya vuelto a fumar.
– b) Si transcurrido un año esa persona sigue sin fumar, calcule la probabilidad de que hubiera seguido la terapia A.
– c) Si transcurrido un año esa persona ha vuelto a fumar, calcule la probabilidad de que hubiera seguido la terapia A
Ejercicios_Resueltos
Matemáticas IES
