-
En el experimento aleatorio consistente en lanzar un dado equilibrado con las caras numeradas del 1 al 6 y observar el resultado se consideran los siguientes sucesos: A: “obtener un número mayor que 4”, B: “obtener un número par”.
a) Escriba los elementos de cada uno de los siguientes sucesos:
; 
; 
; 
; 
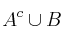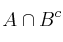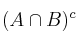
b) Calcule las probabilidades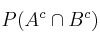 
y 
-
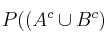
a) Dibuje el recinto del plano definido por las inecuaciones:
; 
; 
; 
; 
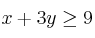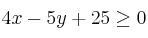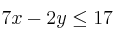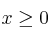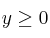
b) Calcule los vértices del mismo
c) Obtenga en dicho recinto los valores máximo y mínimo de la función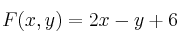 
y los puntos donde se alcanzan.
-
En una empresa han hecho un estudio sobre la rentabilidad de su inversión en publicidad, y han llegado a la conclusión de que el beneficio obtenido, en miles de euros, viene dado por la expresión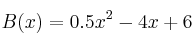 
, siendo x la inversión en publicidad, en miles de euros, con x en el intervalo ![[0,10]](local/cache-TeX/b3c4cde5fd489c54fb5153b585c05c9c.png "[0,10]")
.
– a) ¿Para qué valores de la inversión la empresa tiene pérdidas?
– b) ¿Cuánto tiene que invertir la empresa en publicidad para obtener el mayor beneficio posible?
– c) ¿Cuál es el beneficio si no se invierte nada en publicidad? ¿Hay algún otro valor de la inversión para el cual se obtiene el mismo beneficio?
-
Un estudio sociológico afirma que el 70% de las familias cena viendo la televisión. Se desea contrastar la veracidad de esta afirmación y, para ello, se toma una muestra de 500 familias, en la que se observa que 340 ven la televisión mientras cenan. Decida, mediante un contraste de hipótesis, si la afirmación es cierta con un nivel de significación de 0.01.
-
El director de un banco afirma que la cantidad media de dinero extraído, por cliente, de un cajero automático de su sucursal no supera los 120 euros. Para contrastar esta hipótesis elige al azar 100 extracciones de este cajero y obtiene una media muestral de 130 euros. Se sabe que la cantidad de dinero extraído por un cliente en un cajero automático se distribuye según una ley Normal de media desconocida y desviación típica 67 euros.
– a) Plantee el contraste de hipótesis asociado al enunciado.
– b) Determine la región de aceptación, para un nivel de significación α =0.05.
– c) Con los datos muestrales tomados, ¿existe evidencia estadística para rechazar la hipótesis de este director, con el mismo nivel de significación anterior?
Ejercicios_Resueltos
Matemáticas IES
