EJERCICIOS RESUELTOS - Funciones, Derivadas e Integrales
Análisis matemático: Funciones, Límites, Derivadas e Integrales
Resuelve la intergral 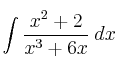
Resuelva la integral 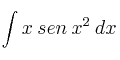
Resuelva la integral 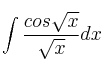
Resuelva la integral 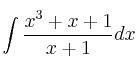
Calcular 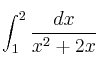
Calcular: 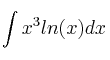
donde ![]() es el logaritmo neperiano de
es el logaritmo neperiano de ![]() .
.
Calcula los siguientes límites aplicando la regla de L’Hôpital tantas veces como te haga falta:
a) ![]()
b) ![]()
c) ![]()
d) ![]()
Calcula las dimensiones de tres campos cuadrados que no tienen ningún lado en común y que satisfacen que el perímetro de uno de ellos es el triple que el de otro y, además, se necesitan 1248 metros de valla para vallar completamente los tres campos, de manera que la suma de las áreas es la mínima posible.
Un granjero quiere bordear un área de ![]() en un campo rectangular y luego dividirlo a la mitad con una barda paralela a un lado del rectángulo. ¿Cómo puede hacerlo para minimizar el costo de la barda?
en un campo rectangular y luego dividirlo a la mitad con una barda paralela a un lado del rectángulo. ¿Cómo puede hacerlo para minimizar el costo de la barda?
 Matemáticas IES
Matemáticas IES
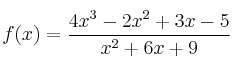 . Calcula:
. Calcula: