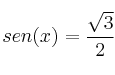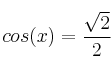EJERCICIOS RESUELTOS - Trigonometría
Trigonometría - 1º Bach. Ciencias
Observamos el punto más alto de un castillo bajo un ángulo de 30 grados sobre la horizontal. Nos acercamos 100 metros y ahora el ángulo es de 45 grados. Halla la altura del castillo.
Demuestra la siguiente igualdad trigonométrica:
![]()
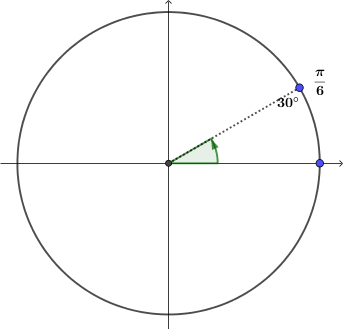
a) Expresa en grados y radianes todos los ángulos entre 0 y 180 que sean múltiplo de 30. Debes expresarlos en la siguiente circunferencia.
b) Expresa en grados y radianes todos los ángulos entre 180 y 360 que sean múltiplo de 45. Debes expresarlos en la siguiente circunferencia.
Sabiendo que 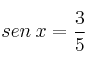 y que
y que 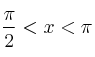 , averigua
, averigua ![]()
Sabiendo que 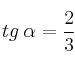 y que
y que ![]() , halla
, halla ![]() y
y ![]()
Sabiendo que 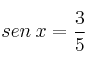 y que
y que 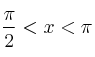 , averigua
, averigua 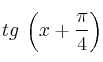
Sabiendo que 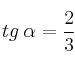 y que
y que ![]() , halla
, halla ![]()
Un ferrocarril une en línea recta dos ciudades A y B. Una tercera ciudad dista de A 22 km. Si el ángulo CAB es de 30º y el
ángulo CBA es de 48º, calcular la distancia de A a B.
 Matemáticas IES
Matemáticas IES