EJERCICIOS RESUELTOS - Funciones y Derivadas
Funciones y derivadas- Matemáticas Aplicadas a las C. S. II
Calcula las asíntotas verticales y horizontales de la función 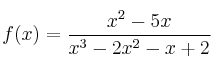
Dada la función ![]() , calcula la derivada de la función en
, calcula la derivada de la función en ![]() utilizando la definición de derivada (calculando un límite).
utilizando la definición de derivada (calculando un límite).
Calcula las derivadas de las siguientes funciones usando las reglas de derivación:
– 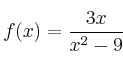
– ![]()
– ![]()
– ![]()
– ![]()
Calcula el área encerrada entre la función ![]() y las rectas
y las rectas ![]() y
y ![]()
Calcula las integrales de las siguientes funciones entre ![]() y
y ![]() aplicando la regla de Barrow:
aplicando la regla de Barrow:
– ![]()
– ![]()
– 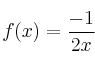
– ![]()
– ![]()
Calcula el área encerrada entre la parábola ![]() y las rectas
y las rectas ![]() y
y ![]()
Se van a imprimir carteles con forma triángulo rectángulo cuyos catetos suman 6 metros. Entre todos los posibles triángulos rectángulos que se pueden formar, optamos por aquel que tenga el área máxima. ¿Qué medidas tendría?
– a) Halle la función derivada de la función 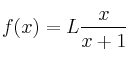 y simplifique el resultado.
y simplifique el resultado.
– b) Obtenga las asíntotas de la función 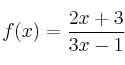
– c) Obtenga los intervalos de concavidad y convexidad de la función 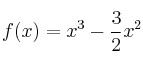
Sea la función 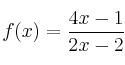
– a) Determine su dominio, los puntos de corte con los ejes, sus asíntotas, y
represéntela gráficamente.
– b) Calcule la ecuación de la recta tangente a la curva ![]() en el punto de abscisa
en el punto de abscisa ![]() .
.
Calcule las derivadas de las siguientes funciones (no es necesario simplificar el resultado):
– a) 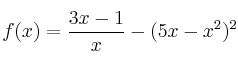
– b) ![]()
– c) ![]()
– d) ![]()
 Matemáticas IES
Matemáticas IES