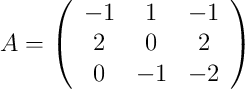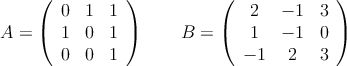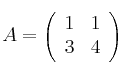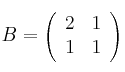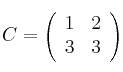EJERCICIOS RESUELTOS - Matrices, Determinantes y Sistemas
Matrices, Determinantes y Sistemas - 2º Bach. Ciencias
Dada la siguiente matriz:
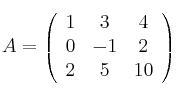
se pide:
a) Halla el determinante de A.
b) Halla el rango de A usando uno cualquiera de los siguientes métodos: Gauss ó determinantes.
Dado el siguiente sistema de ecuaciones:
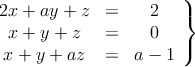
a) Discute el sistema en función de los valores del parámetro ![]()
b) Resuelve el sistema para ![]()
Dado el sistema
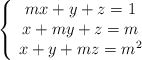
– a) Discute el sistema en función de m.
– b) Resuelve el sistema, si es posible, para m = 1 y m = - 2.
– a) Discute en función del parámetro ![]() el siguiente sistema de ecuaciones.
el siguiente sistema de ecuaciones.
– b) Resuelve el sistema, en caso de ser posible, para ![]()
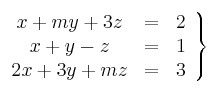
Dado el siguiente sistema:
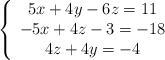
a) Escribe la matriz de los coeficientes, la matriz ampliada, la de las incógnitas y la de los términos independientes. Expresa el sistema en forma matricial.
b) Resuelve el sistema por el método que desees (Gauss o Cramer). A la vista de las soluciones, ¿de qué tipo es el sistema?
 Matemáticas IES
Matemáticas IES