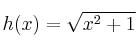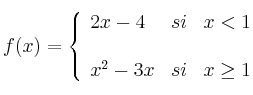EJERCICIOS RESUELTOS - Funciones 4º ESO

Funciones Matemáticas 4º ESO

Calcula los puntos de corte con los ejes de coordenadas de la función $y=x^2-6x+5$

Calcula el dominio de definición de las siguientes funciones:

– a) $f(x) = \sqrt{2x-7}$
– b) $g(x) = \sqrt{-x}$
– c) $h(x) = \sqrt{x^2 + 1}$
– d) $i(x) = \sqrt[3]{2x-1}$

Dada la función cuadrática $f(x)=3x^2-6x+1$

a) Indica su dominio y recorrido.
b) Obtén los puntos de corte con los ejes.
c) Calcula su vértice.
d) Representación gráfica

Solución

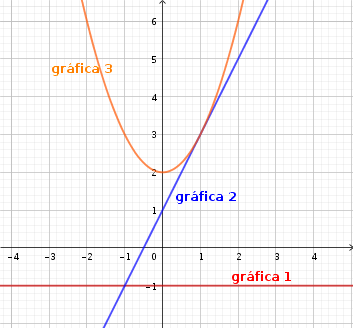
Dadas las siguientes funciones, definidas por su expresión algebraica, selecciona la gráfica que corresponde a cada una e indica de qué tipo de función se trata.

a) $f(x) = -1$
b) $g(x) = 2x+1$
c) $h(x) = x^2+2$

Solución

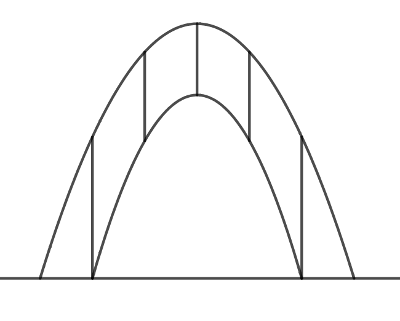
Una estructura metálica tiene la forma de dos arcos parabólicos como muestra la figura. La altura del arco mayor es de 25 metros y su base mide 18 metros, mientras que la altura del arco menor es de 18 metros y su base mide 12 metros. Ambos arcos están unidos por 5 soportes equidistantes. Hallar la longitud total de los soportes.

Solución

Calcula los puntos de corte con los ejes de coordenadas de las siguientes funciones:

– a) 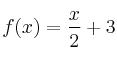$f(x) = \frac{x}{2} + 3$
– b) $f(x) = -3.5x - 5$

Solución

Representa gráficamente las siguientes funciones:

– a) $f(x) = 1.5^x$
– b) $g(x) = 0.75^x$

Solución

Representa gráficamente las funciones:

– a) $f(x) = log (x+5)$
– b) $g(x) = Ln (x)$

Solución

Representa gráficamente la función:

$f(x)= \left\{ \begin{array}{lcc} 2x - 4 & si & x < 1 \\ \\ x^2-3x & si & x \geq 1 \end{array} \right.$

Solución

Lanzamos verticalmente un cohete. La altura $y$ (en metros) a la que se encuentra en cada instante $x$ (en segundos) viene determinada por la función: $y = -5x^2 + 500x$ . Se pide:

– a) Dibuja la gráfica de la función
– b) Indica cuál es su dominio
– c) ¿Cuánto tiempo pasará para que alcance su altura máxima? ¿Cuál será esa altura máxima?
– d) ¿En qué intervalo de tiempo estará a una altura mayor de 4.500 metros?

Más páginas de Ejercicios