EJERCICIOS RESUELTOS - Probabilidad

Probabilidad - Matemáticas 4º ESO

En la siguiente tabla de contingencia se muestran los bomberos de la comunidad valenciana donde se distinguen entre bomberos especialistas y bomberos conductores. También se pueden clasificar por el cuerpo al que pertenecen: Cuerpo de Bomberos, Bomberos Forestales y Bomberos Militares

$\begin{array}{c|ccc|} & Cuerpo B & Forestales & Militares\\ \hline Espec. &185 & 56 & 24 \\ \hline Conductor &74 & 23 & 11 \\ \hline \end{array}$

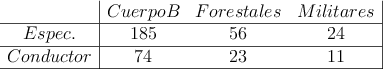
Si escogemos un bombero al azar:

a) ¿Cuál es la probabilidad de que sea un bombero conductor?

b) ¿Cuál es la probabilidad de que sea un bombero especialista?

c) ¿Cuál es la probabilidad de que sea un bombero forestal?

d) ¿Cuál es la probabilidad de que sea un bombero especialista perteneciente al cuerpo de bomberos?

Solución

Se dispone de 2 vías para viajar de $c_1$ a $c_2$ y de 3 vias para viajar de $c_2$ a $c_1$ .
¿De cuantas maneras se puede organizar el viaje de ida y vuelta de $c_1$ a $c_2$ ?

Solución

Indica cuáles de los experimentos siguientes son aleatorios:

– a) Hacer girar una ruleta y observar el número obtenido.
– b) Efectuar una reacción química y determinar los productos obtenidos.
– c) Extraer una bola de una bolsa opaca que contiene bolas rojas, azules y verdes, y mirar el color.
– d) Repartir una mano de 5 cartas cada jugador y mirar las cartas que nos han tocado.
– e) Lanzar una carta a la mesa y observar si cae sobre el dorso o sobre la figura
– f) Calentar agua hasta que entre en ebullición y mirar la temperatura que marca el termómetro.
– g) Extraer una carta de una baraja y anotar el palo al que pertenece.
– h) Arrojar una piedra al vacío y medir su aceleración.
– i) Medir la longitud de una circunferencia de radio 3.
– j) Abrir las compuertas de un estanque lleno de agua y anotar lo que ocurre.

Solución

Dado el experimento aleatorio "extraer una carta de una baraja española", se consideran los sucesos:
A = "salir as"
B = "salir rey"
C = "salir copas"
D = "salir figura"

Indica si las siguientes parejas de sucesos son compatibles o incompatibles:
$A \: y \: B$ , $A \: y \: C$ , $A \: y \: D$ , $B \: y \: C$ , $B \: y \: D$ , $C \: y \: D$ , $A \: y \: \overline{A}$ ,

Solución

De una urna que contiene 15 bolas rojas y 10 verdes, extraemos dos bolas consecutivamente. Halla la probabilidad de que ambas sean rojas.

– Con Reemplazamiento (o reintegro)
– Sin reemplazamiento (sin reintegro)

Solución

Dado el experimento aleatorio "lanzar un dado", se pide:

– Espacio Muestral
– Describe dos sucesos contrarios
– Son contrarios los sucesos $A=\{2,3,4,5\}$ y $B=\{1,5,6\}$

Solución

Dado el experimento aleatorio "lanzar un dado", describe el Espacio Muestral . Si consideramos los sucesos $A=\{1,2,3\}$ , $B=\{2,4\}$ y $C=\{4,5,6\}$ , describe los siguientes sucesos:
$A \cup B$ , $A \cap C$ , $A \cup C$ , $B \cap C$ , $B \cup C$ , $A \cup \overline{A}$ , $A \cap B$ , $\overline{B} \cap \overline{C}$

Solución

Disponemos de una urna con 5 bolas negras, 3 rojas y 7 azules. Extraemos una bola al azar. Se pide:

– Espacio Muestral
– Probabilidad de obtener bola negra
– Probabilidad de obtener roja o azul

Solución

Lanzamos tres monedas. Se pide:

– Espacio Muestral
– Probabilidad de obtener al menos una cruz
– Probabilidad de no obtener ninguna cruz

Solución

Disponemos de una urna que contiene las letras N , O , N , O , N. Extraemos dos letras al azar. Calcula la probabilidad de que salga "NO".

Más páginas de Ejercicios