EJERCICIOS RESUELTOS - Funciones II
Funciones (conociendo Derivadas) - 1º Bach. Ciencias
Estudie la monotonía de la función ![]()
Estudia la curvatura y puntos de inflexión de la función ![]()
Halla las asíntotas horizontales de las funciones:
– 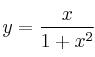
– 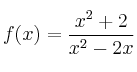
Halla la asíntota oblicua de la función:
– 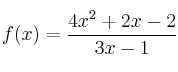
Halla las asíntotas horizontales de las funciones:
– 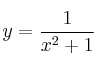
– 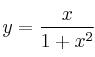
– 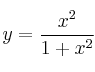
– 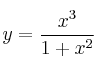
Calcula las asíntotas verticales y estudia el comportamiento en sus proximidades, de la función
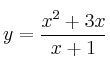
Sea la función 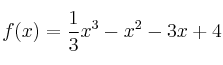
– a) Encuentre los puntos críticos de ![]() por medio del criterio de la primera derivada
por medio del criterio de la primera derivada
– b) Halle los intervalos donde la función es creciente y decreciente, así como los puntos máximos y mínimos
– c) Determine los puntos de inflexión
– d) Trace la gráfica de la función ![]()
Para la función 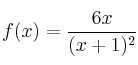 se pide:
se pide:
– a) Dominio
– b) Corte con los ejes
– c) Monotonía y Extremos
– d) Curvatura y Puntos de Inflexión
– e) Representación gráfica teniendo en cuenta los apartados anteriores
Realiza un estudio global (dominio, simetrías, corte con los ejes, asíntotas, monotonía, extremos y representación gráfica) de la función:
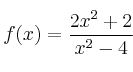
Realiza un estudio global (dominio, simetrías, corte con los ejes, asíntotas, monotonía, extremos y representación gráfica) de la función:
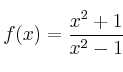
 Matemáticas IES
Matemáticas IES