-
En una carpintería, que consta de tres secciones, se construyen mesas y conjuntos de 4 sillas. En la primera sección se cortan las piezas que conforman los muebles, invirtiéndose una hora en el conjunto de las 4 sillas y tres horas en la mesa. En la segunda sección se realiza el ensamblaje de las piezas, empleándose 1 hora y 20 minutos, tanto para las sillas como para la mesa. Por último, en la tercera sección se pulen los muebles, tardándose 2 horas y 30 minutos en finalizar las 4 sillas y sólo 8/7 de hora en la mesa. Debido a las características de la empresa, sólo se puede trabajar un máximo de 61 horas semanales en las secciones 2ª y 3ª y 60 horas en la 1ª. Sabiendo que las ganancias por el conjunto de las 4 sillas y la mesa son respectivamente, 800 € y 600 €, organiza tú mismo cómo debiera ser la producción para que así los beneficios fuesen máximos.
-
Cierta compañía produce dos tipos de alimentos para perros, marcas A y B, respectivamente. Cada lata de la marca A contiene 200 g de carne y 100 g de harina. La marca B contiene 140 g de carne y 160 g de harina por lata.
Las instalaciones pueden manipular un máximo de 78 kg. de carne y 48 kg. de harina por hora. Si el beneficio obtenido de la marca A es de 300 u.m. (unidades monetarias) por lata y el de la marca B es de 240 u.m. por lata, ¿Cuántas latas de cada marca deben producirse por hora para maximizar el beneficio?
Averigua cómo se alcanzará el beneficio máximo.
-
Dado el sistema
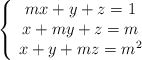
– a) Discute el sistema en función de m.
– b) Resuelve el sistema, si es posible, para m = 1 y m = - 2.
-
Dadas las matrices:
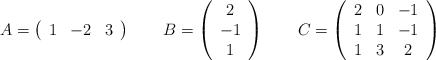
– a) Justifica si la matriz C tiene inversa
– b) Halla la inversa de C
– c) Resuelve la ecuación matricial 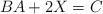
-
Sabiendo que A y B son dos matrices de orden 2, tales que |A| = - 2 y |B| = 4, calcula:
– a) 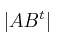
– b) 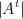
– c) 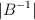
– d) 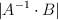
– e) 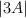
 Ejercicios_Resueltos
Ejercicios_Resueltos