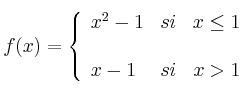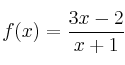EJERCICIOS RESUELTOS - Funciones (I)
Funciones (I) - 1º Bachillerato de Ciencias
Halla el valor de 
para que la siguiente función sea continua.
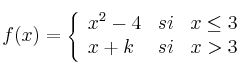
Calcula los puntos de corte con los Ejes de Coordenadas de las siguientes funciones:
– 
– 
Halla los puntos de corte con los Ejes de Coordenadas de la función:
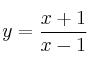
Halla los puntos de corte con los Ejes de Coordenadas de la función:
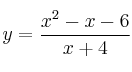
El beneficio esperado por una empresa, en los próximos 8 años, viene indicado por la función:
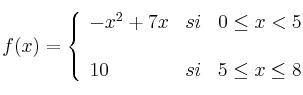
El tiempo (x) está expresado en años y el Beneficio f(x) viene expresado en millones de euros.
– a) Representa gráficamente la función
– b) Explica la evolución del beneficio en esos 8 años
– c) ¿Cuándo se espera un beneficio de 11,25 millones de euros?
Dada la función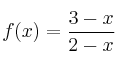 
, se pide:
– a) Representación gráfica
– b) Monotonía (crecimiento y decrecimiento) y Asíntotas
Halla el dominio de la función
