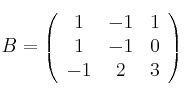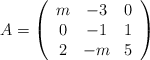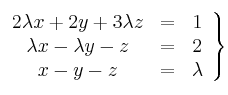EJERCICIOS RESUELTOS - Matrices, Determinantes y Sistemas
Matrices, Determinantes y Sistemas - 2º Bach. Ciencias
Dada la siguiente matriz:
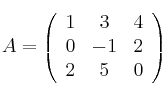
Determina si es posible obtener su inversa o no, y en caso afirmativo halla ![]()
Sea la matriz
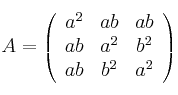
– a) Sin utilizar la regla de Sarrus, calcular el determinante de dicha matriz
– b) Estudiar el rango de A en caso de que ![]()
Dadas las siguientes matrices:
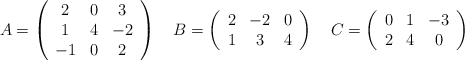
Indica razonadamente cuáles de las siguientes operaciones se pueden hacer y cuáles no y realiza todas aquellas que sí se puedan:
– a) ![]()
– b) ![]()
– c) ![]()
– d) ![]()
– e) ![]()
– f) ![]()
La gerencia de una sociedad de inversiones tiene un fondo 200.000 USD para invertir en acciones. A fin de alcanzar un nivel aceptable de riesgo, las acciones consideradas se han clasificado en tres categorías: de alto, mediano y bajo riesgo. La gerencia estima que las acciones de alto riesgo tendrán una tasa de rendimiento del 15% anual; las de riesgo medio, 10% anual, y las de bajo riesgo, 6% anual. La inversión en las acciones de bajo riesgo será el doble de la suma invertida en las otras dos categorías. El objetivo de la inversión es tener una tasa promedia de rendimiento del 9% anual sobre la inversión total. ¿Cuánto se debe invertir en cada tipo de acción?
De las matrices:
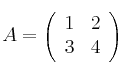 ,
,
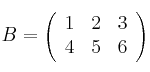 ,
,
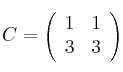 y
y
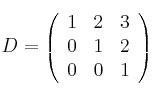
determina cuáles tienen inversa y en los casos en que exista, calcula el determinante de dichas inversas.
Considera
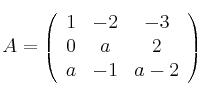 ,
,
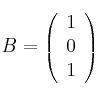 y
y
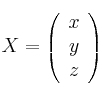
– (a) Determina el rango de ![]() en función del parámetro
en función del parámetro ![]()
– (b) Discute en función de ![]() en sistema, dado en forma matricial
en sistema, dado en forma matricial ![]()
– (c) Resuelve ![]() en los casos en que sea compatible indeterminado.
en los casos en que sea compatible indeterminado.
 Matemáticas IES
Matemáticas IES
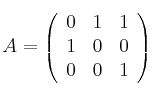 ;
;