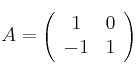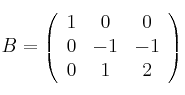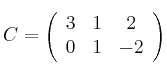EJERCICIOS RESUELTOS - Matrices, Determinantes y Sistemas
Matrices, Determinantes y Sistemas - 2º Bach. Ciencias
Considera el sistema de ecuaciones:
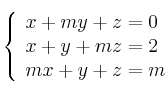
– (a) ¿Para qué valor de ![]() el sistema tiene al menos dos soluciones?
el sistema tiene al menos dos soluciones?
– (b) ¿Para qué valores de ![]() el sistema admite solución en la que
el sistema admite solución en la que ![]() ?
?
Considera el sistema de ecuaciones
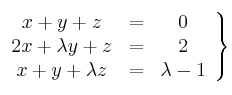
– a) Determina el valor de ![]() para que el sistema sea incompatible.
para que el sistema sea incompatible.
– b) Resuelva el sistema para ![]()
– (a) Calcula el valor de ![]() para el que la matriz
para el que la matriz
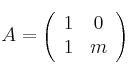
verifica la relación ![]() y determina
y determina ![]() para dicho valor de
para dicho valor de ![]()
– (b) Si ![]() es una matriz cuadrada que verifica la relación
es una matriz cuadrada que verifica la relación ![]() , determina la expresión de
, determina la expresión de ![]() en función de
en función de ![]() y de
y de ![]() .
.
Resuelva el siguiente sistema de ecuaciones para ls valores de ![]() que lo hacen compatible:
que lo hacen compatible:
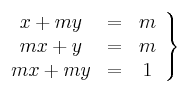
Considera la matriz
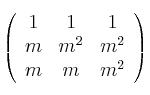
– a) Halla los valores del parámetro ![]() para los que el rango de A es menor que 3
para los que el rango de A es menor que 3
– b) Estudia si el sistema
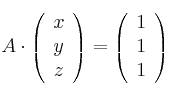 tiene solución para cada uno de los valores de m obtenidos en el apartado anterior.
tiene solución para cada uno de los valores de m obtenidos en el apartado anterior.
– (a) Determina razonadamente los valores del parámetro ![]() para los que el siguiente sistema de ecuaciones tiene más de una solución:
para los que el siguiente sistema de ecuaciones tiene más de una solución:
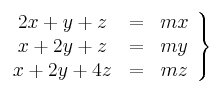
– (b) Resuelve el sistema anterior para el caso ![]() y para el caso
y para el caso ![]() .
.
Dada la matriz
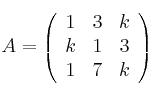
– (a) Estudia el rango de ![]() en función de los valores del parámetro
en función de los valores del parámetro ![]() .
.
– (b) Para ![]() , halla la matriz inversa de
, halla la matriz inversa de ![]() .
.
Considera las matrices:
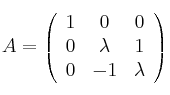
![]() y
y ![]()
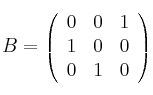
– a) ¿Hay algún valor de ![]() para el que
para el que ![]() no tiene inversa?
no tiene inversa?
– b) Para ![]() , resuelve la ecuación matricial
, resuelve la ecuación matricial ![]()
Dadas las matrices
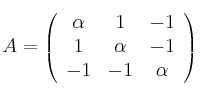
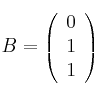
– a) Calcula el rango de ![]() dependiendo de los valores de
dependiendo de los valores de ![]()
– b) Para ![]() , resuelve la ecuación matricial
, resuelve la ecuación matricial ![]()
 Matemáticas IES
Matemáticas IES