EJERCICIOS RESUELTOS - Probabilidad
Probabilidad - Matemáticas 4º ESO
Extraemos al azar una ficha de dominó. Calcula:
– Probabilidad de que la suma de puntos sea 6
– Probabilidad de que la suma de puntos sea menor que 4
– Probabilidad de sacar un doble
En el experimento aleatorio "lanzar dos dados" consideramos los siguientes sucesos:
– A = "La suma de puntos obtenidos es 5"
– B = "En un dado ha salido 4"
– C = "Mismo resultado en ambos dados"
Halla los sucesos elementales y la probabilidad de los siguientes sucesos:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
Describe el Espacio Muestral al lanzar 3 monedas. Consideremos los sucesos:
A = "obtener exactamente dos caras"
B = "obtener al menos una cruz"
Describe los sucesos:
![]() ,
, ![]() ,
, ![]() ,
, ![]()
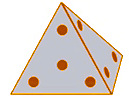
Realizamos el experimento aleatorio de lanzar dos dados tetraédricos (4 caras que son triángulos equiláteros) cuyas caras están numeradas del 1 al 4, y sumamos las puntuaciones ocultas de ambos dados. Considerando los sucesos:
– A = "la suma es impar"
– B = "la suma es múltiplo de 3"
– C = "la suma es menor que 5"
Calcula las siguientes probabilidades:
a) ![]()
b) ![]()
c) ![]()
d) ![]()
e) ![]()
f) ![]()
Las probabilidades que tienen dos estudiantes R, W de resolver un mismo problema, por separado, son ![]() y
y ![]() respectivamente. Si se sabe que ambos estudiantes, trabajando al mismo tiempo (suma delas probabilidades), no logran resolverlo. Entonces, ¿cuáles valores son posibles para m?
respectivamente. Si se sabe que ambos estudiantes, trabajando al mismo tiempo (suma delas probabilidades), no logran resolverlo. Entonces, ¿cuáles valores son posibles para m?
– A) 2 y 4.
– B) 3 y 2.
– C) 4 y 3.
– D) 5 y 3.
Disponemos de dos urnas. En la primera hay 6 bolas, cada una tiene una de las letras de la palabra PREMIO. En la segunda urna, cada bola tiene una de las letras de la palabra SUERTE. Extraemos una bola al azar de cada urna. Indica, para cada una de las urnas:
– Espacio Muestral
– Los Sucesos Elementales
– ¿Tienen la misma probabilidad los sucesos elementales?
– Probabilidad de obtener una vocal
Disponemos de dos ruletas de colores (se muestran en la siguiente imagen). Calcula, para cada una de ellas las probabilidades de salir Rojo, Verde, Amarillo y Azul.
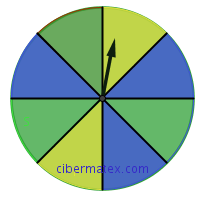
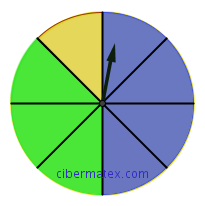
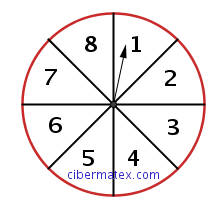
Disponemos de una ruleta como la que muestra la figura. Nos piden:
– Probabilidad de obtener número par
– Probabilidad de obtener número primo
– Probabilidad de obtener el número 5 ó superior
– Probabilidad de obtener el número 7
Indica si podemos aplicar la regla de Laplace en los siguientes experimentos aleatorios:
– Lanzamiento de un dado no trucado
– Lanzamiento de una chincheta
– Lanzamiento de un dardo contra las siguientes dianas:
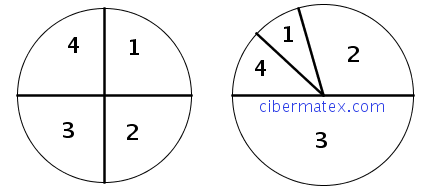
Consideremos el experimento aleatorio "anotar la última cifra de un sorteo". Determina el Espacio Muestral y los sucesos: A="número menor que 5" y B="número par". Describe los siguientes sucesos:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
 Matemáticas IES
Matemáticas IES