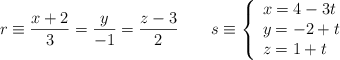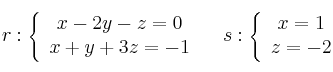EJERCICIOS RESUELTOS - Geometría en el Espacio
Ejercicios de Geometría en el espacio. Bachillerato
Dados los vectores ![]() ,
, ![]() .
. ![]() ,
, ![]() , calcula
, calcula ![]() de forma que se cumpla:
de forma que se cumpla: ![]()
Halla el ángulo que forman los vectores ![]() y
y ![]()
Calcula el área del triángulo de vértices ![]() ,
, ![]()
y ![]()
Los puntos ![]() ,
, ![]() y
y ![]() son tres de los vértices de un tetraedro. El cuarto vértice D está contenido en la recta r que pasa por el punto
son tres de los vértices de un tetraedro. El cuarto vértice D está contenido en la recta r que pasa por el punto ![]() y es perpendicular al plano
y es perpendicular al plano ![]() que contiene a los puntos A, B y C.
que contiene a los puntos A, B y C.
– a) Calcule la ecuación del plano que contiene a los puntos A, B y C.
– b) Calcule la ecuación de la recta r que pasa por el punto ![]() y es perpendicular al plano
y es perpendicular al plano ![]()
– c) Calcule las coordenadas del vértice D sabiendo que el volumen del tetraedro es 18.
Demuestre que los tres puntos (1,-1, 3), (2, 1 ,7) y (4, 2, 6) son los vértices de un triángulo rectángulo y calcule su área.
Halla la distancia entre las rectas:
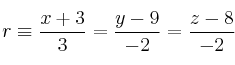
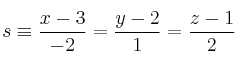
 Matemáticas IES
Matemáticas IES