-
El peso de las peras de una cosecha se distribuye según una ley normal de media 115 gramos y desviación típica 25 gramos.
– a) ¿Cuál es la probabilidad de que una pera elegida al azar pese más de 120 gramos?
– b) ¿Cuál es la probabilidad de que el peso medio de una muestra de 64 peras esté entre 112 y 119 gramos?
-
Una encuesta realizada sobre 40 aviones comerciales revela que la antigüedad media de estos es de 13,41 años, con una desviación típica de 8,28 años. Se pide:
– a) ¿Entre qué valores, con un 
de confianza, se encuentra la auténtica media de la flota comercial?
– b) Si se quiere obtener un nivel de confianza del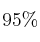 
cometiendo el mismo error de estimación que en el apartado anterior y suponiendo también que la desviación típica muestral es de 8,28 años, ¿cuántos elementos debería componer la muestra?
-
Un estudio realizado sobre 100 usuarios revela que un automóvil recorre anualmente un promedio de 15200 km con una desviación típica de 2250 km.
– a) Determine un intervalo de confianza, al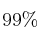 
, para la cantidad promedio de kilómetros recorridos.
– b) ¿Cuál debe ser el tamaño mínimo de la muestra para que el error cometido no sea superior a 500 km, con igual confianza?
-
La altura de los jóvenes andaluces se distribuye según ley normal de media desconocida y varianza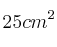 
. Se ha tomado una muestra aleatoria, y con una confianza de 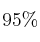, se ha construido un intervalo para la media poblacional cuya amplitud es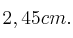 
– a) ¿Cuál ha sido el tamaño de la muestra seleccionada?
– b) Determina el límite superior y el inferior del intervalo de confianza si la muestra tomada dio una altura media de 170 cm
-
Queremos obtener la media de una variable que se distribuye normalmente con una desviación típica de 3,2. Para ello, se toma una muestra de 64 individuos obteniéndose una media de 32,5. ¿Con qué nivel de confianza se puede afirmar que la media de la población está entre 31,5 y 33,5?
Si la desviación típica de la población fuera 3, ¿Cuál es el tamaño mínimo que debería tener la muestra con la cual estimamos la media poblacional, si queremos que el nivel de confianza sea de 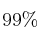y el error admisible no supere el valor de 0,75?
Ejercicios_Resueltos
Matemáticas IES
