Trigonometría - Matemáticas 4º ESO

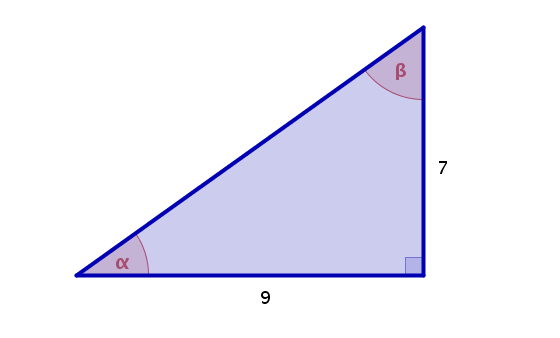
Calcula el valor de las razones trigonométricas (seno, coseno y tangente) de todos los ángulos de un triángulo rectángulo de catetos 7m y 9m.

Resuelve un triángulo isósceles sabiendo que el lado desigual mide 20 cm. y uno de sus ángulos mide 30 grados.

Sabiendo que y que , calcula las demás razones trigonométricas del ángulo

Calcula seno y coseno de un ángulo del tercer cuadrante sabiendo que su tangente es

Calcula las razones trigonométricas de todos los ángulos de un triángulo de lados 12, 13 y 5

Sin usar la calculadora y sabiendo que , y , calcula:

 
 
 
 

Calcula, sin usar la calculadora, las razones trigonométricas de los siguientes ángulos:

 a)
 b)
 c)
 d)

Sin usar la calculadora, averigua las razones trigonométricas de los siguientes ángulos:

 a)
 b)
 c)
 d)

Calcula el valor de las razones trigonométricas (seno, coseno y tangente) de todos los ángulos del siguiente triángulo

Calcula el valor del ángulo sabiendo que