EJERCICIOS RESUELTOS - Funciones, Derivadas e Integrales
Análisis matemático: Funciones, Límites, Derivadas e Integrales
Descomponer el número 12 en dos sumandos positivos de forma que el producto del primero por el cuadrado del segundo sea máximo.
Dada la función 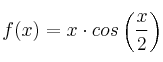 , calcula una primitiva que pase por el punto
, calcula una primitiva que pase por el punto ![]()
Un trozo de alambre de 10 metros de largo se corta en dos partes. Una se dobla para formar un cuadrado y la otra para formar un triángulo equilátero. Determine cómo debe cortarse el alambre de modo que el área total encerrada sea:
– a) Máxima
– b) Mínima
Queremos fabricar una caja sin tapa con base cuadrada y con un área de ![]() . Si queremos que el volumen sea máximo, ¿cuáles serían sus dimensiones?
. Si queremos que el volumen sea máximo, ¿cuáles serían sus dimensiones?
Un industrial desea construir una caja abierta, es decir sin tapa, de base cuadrada y superficie total 108 centímetros cuadrados. ¿Qué dimensiones tendrá la caja de volumen máximo?
Sea ![]() la función definida por
la función definida por ![]()
– a) Halla la ecuación de la recta normal a la gráfica de ![]() en el punto de abcisa
en el punto de abcisa ![]()
– b) Determina el punto de la gráfica en el que la recta tangente es perpendicular a la recta ![]()
Represente gráficamente la función ![]()
Sea ![]() la función definida para
la función definida para ![]() por
por 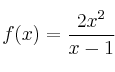
– (a) Determina las asíntotas de la gráfica de ![]()
– (b) Determina los intervalos de crecimiento y decrecimiento y los extremos relativos de ![]()
– (c) Esboza la gráfica de ![]()
Sea la función ![]() definida por:
definida por:
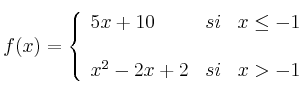
– (a) Esboza la gráfica de ![]()
– (b) Calcula el área de la región limitada por la gráfica de ![]() , el eje de abcisas y la recta
, el eje de abcisas y la recta ![]()
Siendo ![]() el logaritmo neperiano de
el logaritmo neperiano de ![]() , considera la función
, considera la función ![]() definida por
definida por ![]() . calcula:
. calcula:
– (a) 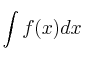
– (b) Una primitiva de ![]() cuya gráfica pase por el punto
cuya gráfica pase por el punto ![]()
 Matemáticas IES
Matemáticas IES