EJERCICIOS RESUELTOS - Geometría en el Espacio
Ejercicios de Geometría en el espacio. Bachillerato
A la empresa de obras públicas North SA se le ha encargado la construcción de una autovía que una dos importantes ciudades andaluzas. El recorrido de la misma pasa por una montaña y por razones económicas se ha decidido atravesarla construyendo un túnel. Tú puedes echar una mano a los ingenieros implicados en el proyecto a la hora de afrontar los cálculos matemáticos necesarios para realizar la obra.
Se pide:
1. El túnel sigue la trayectoria marcada por los puntos A(-1,1,1) y B(1,2,1). Halla la recta que pasa por estos, a la cual vamos a llamar r.
2. Las laderas de la montaña vienen dadas por lo planos cuyas ecuaciones son:
![]() y
y ![]()
Halla los puntos de intersección de la recta r con los planos, vamos a nombrar a estos puntos como E(entrada) y S(salida).
3. Halla la longitud del túnel (distancia entre E y S).
4. En la cima de la montaña se va a trazar otra carretera cuya trayectoria viene determinada por la intersección de los planos ![]() y
y ![]() . Halla la intersección de los mismos, a la cual vamos a llamar s.
. Halla la intersección de los mismos, a la cual vamos a llamar s.
5 Para la ventilación del túnel se va a crear un pozo de impulsión que conecta la cima de la montaña con el túnel y se quiere saber cuál es la longitud del mismo, el pozo sigue la perpendicular que une las rectas r y s. Halla la distancia entre ambas rectas.
Dados los vectores ![]() y
y ![]() , calcula el producto vectorial
, calcula el producto vectorial ![]() y comprueba que
y comprueba que ![]() y
y ![]()
Halla la ecuación de la recta que pasa por el punto ![]() y es perpendicular a cada una de las rectas
y es perpendicular a cada una de las rectas 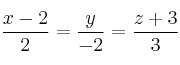 y
y 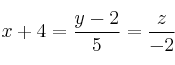
Dado el punto ![]() , el plano
, el plano ![]() y la recta
y la recta ![]()
a) Halla la ecuación del plano que pasa por P y contiene a r
b) Halla la ecuación de la recta que pasa por P, es paralela a ![]() y corta a r
y corta a r
Comprueba si las siguientes rectas son ortogonales
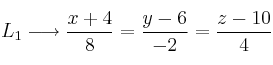
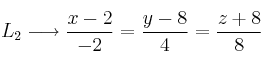
Obtenga su gráfica usando geogebra, octave u otro software
Considera los puntos:
![]() ,
, ![]() ,
, ![]() y
y ![]()
Halla ![]() y
y ![]() sabiendo que la recta que pasa por
sabiendo que la recta que pasa por ![]() y
y ![]() corta perpendicularmente a la recta que pasa por
corta perpendicularmente a la recta que pasa por ![]() y
y ![]()
Halla la ecuación del plano que pasa por el punto ![]() , es perpendicular al plano
, es perpendicular al plano ![]() y es paralelo a la recta
y es paralelo a la recta
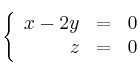
Sabiendo que las rectas
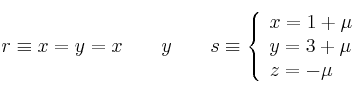
se cruzan, halla los puntos ![]() y
y ![]() , de
, de ![]() y
y ![]() respectivamente, que están a mínima distancia.
respectivamente, que están a mínima distancia.
Considera el punto ![]() , el plano
, el plano ![]() y la recta
y la recta 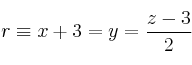 .
.
– (a) Determina la ecuación del plano que pasa por ![]() y contiene a
y contiene a ![]() .
.
– (b) Determina la ecuación de la recta que pasa por ![]() , es paralela a
, es paralela a ![]() y corta a
y corta a ![]() .
.
Considera el punto ![]() , el plano
, el plano ![]() y la recta
y la recta 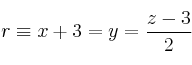 .
.
– (a) Determina la ecuación del plano que pasa por ![]() y contiene a
y contiene a ![]() .
.
– (b) Determina la ecuación de la recta que pasa por ![]() , es paralela a
, es paralela a ![]() y corta a
y corta a ![]() .
.
 Matemáticas IES
Matemáticas IES