EJERCICIOS RESUELTOS - Geometría en el Espacio

Ejercicios de Geometría en el espacio. Bachillerato

Dados los puntos $A(3,-2,-2)$ , $B(1,0,1)$ y $C(2,1,-1)$
y el plano 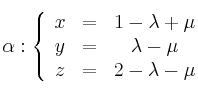$\alpha : \left\{ \begin{array}{ccc} x & = & 1 - \lambda + \mu \\ y & = & \lambda - \mu \\ z & = & 2 - \lambda - \mu \end{array} \right.$

Se pide:

a) Comprueba si los puntos A, B y C pertenecen al plano.

b) Halla la ecuación general del plano.

Solución

Escriba las ecuaciones paramétricas, continua e implícita de la recta que pasa por los puntos $A(1,2,4)$ y $B(0,-2, -5)$

Solución

Dados los puntos $A(3, -1, 0)$ y $B(1, -5, 3)$ se considera la recta $r$ que pasa por ambos. Se pide:

a) Halla un vector director de $r$ .

b) Obtén la ecuación vectorial, paramétrica, continua e implícita (o general) de $r$ .

Solución

Dados el punto $P(3, -2, 1)$ y los vectores $\vec{v}=(2,4,-1)$ y $\vec{w}=(0,-2,3)$ se pide:

a) Halla la ecuación vectorial, paramétrica e implícita (o general) del plano $\pi$ que forman.

b) Comprueba si los puntos $A(3, 2, 1)$ y $B(2, 3, -9)$ pertenecen o no al plano $\pi$ .

Solución

Considera la recta r que pasa por el punto $A(1,-2,5)$ y lleva la dirección del vector $\vec{v}=(-2,-2,0)$
Se pide:

a) Halla su ecuación paramétrica.

b) Halla su ecuación continua.

c) Halla su ecuación implícita.

d) Estudia la posición relativa de la recta r respecto a la s:
$\frac{x-3}{-2}=\frac{y-3}{2}=z-1$

Solución

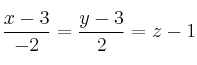
Halla los valores de $m$ y $n$ para que los siguientes puntos estén alineados:
$P(7,-1,m)$ , $Q(8,6,3)$ , $R(10,n,9)$

Solución

Los puntos $A(1,3,-1)$ , $B(2,0,2)$ y $C(4,-1,-3)$ son los vértices consecutivos de un paralelogramo. Halla el cuarto vértice y el centro del paralelogramo

Solución

Dadas las rectas
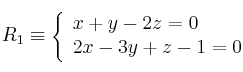$R_1 \equiv \left\{ \begin{array}{lll} x+y-2z=0 \\2x-3y+z-1=0 \end{array} \right.$ y $R_2 \equiv \left\{ \begin{array}{lll} x= 3 \lambda \\ y = 1 - 2\lambda \\ z = 2 +\lambda \end{array} \right.$
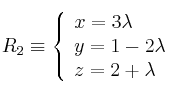
– a) Halla los puntos de corte entre $R_2$ y el plano $\pi : x-3y-2z=2$
– b) Halla la ecuación de un plano que sea perpendicular a $R_1$ y que pase por el punto de corte hallado en el apartado a)

Solución

Considera los puntos $A(1,0,2)$ , $B(-1,3,1)$ y $C(2,1,2)$

– (a) Halla la ecuación del plano que contiene a $A$ , $B$ y $C$
– (b) Halla el área del triángulo de vértices $A$ , $B$ y $C$

Solución

Dados los puntos $A(1,2,3)$ , $B(1,0,0)$ y $C(0,1,1)$ , se pide:

– a) Ecuación del plano $\pi$ que pasa por $A$ , $B$ y $C$
– b) Vector normal al plano $\pi$
– c) Ecuación de una recta perpendicular al plano $\pi$ y que pase por el punto $(0,0,1)$

Más páginas de Ejercicios