EJERCICIOS RESUELTOS - Matrices, Determinantes y Sistemas
Matrices, Determinantes y Sistemas - 2º Bach. Ciencias
Sean las matrices
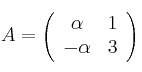
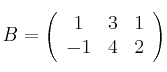
– a) Calcula los valores de ![]() para los que la matriz inversa de A es
para los que la matriz inversa de A es ![]()
– b) Para ![]() , determina la matriz
, determina la matriz ![]() que verifica la ecuación
que verifica la ecuación ![]() , siendo
, siendo ![]() la matriz traspuesta de
la matriz traspuesta de ![]() .
.
Considera el sistema de ecuaciones
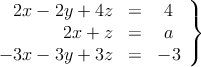
– a) Discútelo según los valores del parámetro ![]()
– b) Resuélvelo cuando sea posible
Sean ![]() y
y ![]() dos matrices cuadradas de orden 3 cuyos determinantes son
dos matrices cuadradas de orden 3 cuyos determinantes son 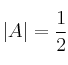 y
y ![]() . Halla:
. Halla:
– a) ![]()
– b) ![]()
– c) ![]()
– d) ![]()
– e) rango(B)
Dado el sistema de ecuaciones lineales
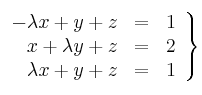
– a) Clasifica el sistema según los valores del parámetro ![]()
– b) Resuelve el sistema para ![]()
Dada la matriz
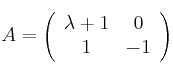
– a) Determina los valores de ![]() para los que la matriz
para los que la matriz ![]() no tiene inversa.
no tiene inversa.
– b) Para ![]() , halla la matriz
, halla la matriz ![]() que verifica la ecuación
que verifica la ecuación ![]() , siendo
, siendo ![]() la matriz identidad de orden 2.
la matriz identidad de orden 2.
Considera las matrices
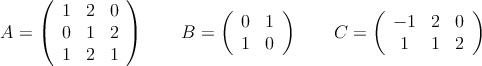
Determina, si existe, la matriz ![]() que verifica
que verifica ![]() , siendo
, siendo ![]() la matriz traspuesta de
la matriz traspuesta de ![]()
Considera el sistema de ecuaciones
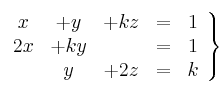
– a) Clasifica el sistema según los valores del parámetro ![]()
– b) Resuélvelo para ![]()
– c) Resuélvelo para ![]()
Considera las matrices
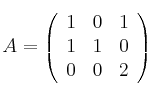 y
y
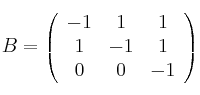
– (a) Halla, si es posible, ![]() y
y ![]()
– (b) Halla el determinante de ![]() siendo
siendo ![]() la matriz traspuesta de
la matriz traspuesta de ![]()
– (c) Calcula la matriz ![]() que satisface
que satisface ![]()
Considera las siguientes matrices
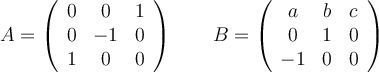
– a) Determina, si existen, los valores de a, b y c para los que las matrices A y B conmutan
– b) Calcula ![]() ,
, ![]() ,
, ![]() y
y ![]()
– c) Calcula, si existe, la matriz inversa de ![]()
Considera el siguiente sistema de ecuaciones lineales
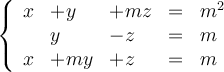
– a) Discute el sistema según los valores del parámetro ![]()
– b) Resuélvelo para ![]() . Para dicho valor de
. Para dicho valor de ![]() , calcula, si es posible, una solución en la que
, calcula, si es posible, una solución en la que ![]()
 Matemáticas IES
Matemáticas IES