EJERCICIOS RESUELTOS - Matrices, Determinantes y Sistemas
Matrices, Determinantes y Sistemas - 2º Bach. Ciencias
Calcula todas las matrices 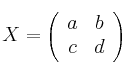 tales que
tales que ![]() , tienen determinante 1 y cumplen
, tienen determinante 1 y cumplen ![]() , siendo
, siendo 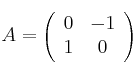
Dadas las matrices 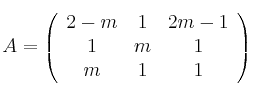 ,
, 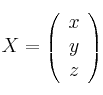 ,
, 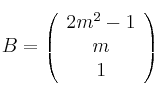 , considera el sistema de ecuaciones lineales dado por
, considera el sistema de ecuaciones lineales dado por ![]() , donde
, donde ![]() ,
, ![]() denotan las traspuestas. Discútelo según los distintos valores de m
denotan las traspuestas. Discútelo según los distintos valores de m
Se consideran las matrices
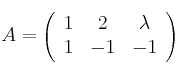
,
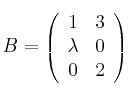
donde ![]() es un número real.
es un número real.
– a) Encontrar los valores de ![]() para los que la matriz
para los que la matriz ![]() tiene inversa
tiene inversa
– b) Dados ![]() y
y ![]() números reales cualesquiera, ¿puede ser el sistema
números reales cualesquiera, ¿puede ser el sistema 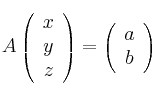 compatible determinado con
compatible determinado con ![]() la matriz del enunciado?.
la matriz del enunciado?.
La liga de fútbol de un cierto país la juegan 21 equipos a doble vuelta. Este año, los partidos
ganados valían 3 puntos, los empatados 1 punto y los perdidos 0 puntos. En estas condiciones, el equipo campeón de liga obtuvo 70 puntos. Hasta el año pasado los partidos ganados valían 2 puntos y el resto igual. Con el sistema antiguo, el actual campeón hubiera obtenido 50 puntos. ¿Cuantos partidos gano, empató y perdió el equipo campeón?
Dado el siguiente sistema:
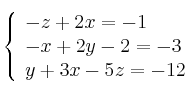
– a) Escribe la matriz de los coeficientes, la matriz ampliada, la de las incógnitas y la de los términos independientes. Expresa el sistema en forma matricial
– b) Resuelve el sistema por el método que desees (Cramer o Gauss). A la vista de las soluciones, ¿de qué tipo es el sistema?
Resuelve por la regla de Cramer el siguiente sistema de ecuaciones
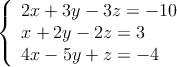
Resuelve por el método de Gauss el siguiente sistema de ecuaciones
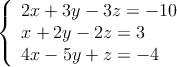
Usa la regla de Cramer para resolver el siguiente sistema de ecuaciones
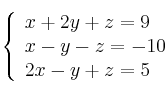
Discute el siguiente sistema en función de los valores del parámetro ![]()
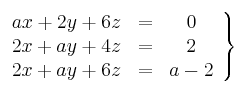
 Matemáticas IES
Matemáticas IES
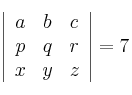 ,
,