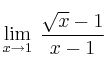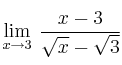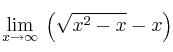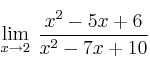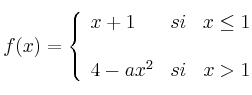EJERCICIOS RESUELTOS - Funciones (I)
Funciones (I) - 1º Bachillerato de Ciencias
Calcula los siguientes límites de funciones:
– 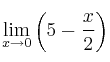
– ![]()
– 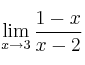
– ![]()
Estudie la continuidad de la función 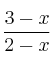
Calcula los puntos de corte con los ejes de coordenadas de la función ![]()
Indica los puntos donde gráfica de la función ![]() corta a los ejes de coordenadas
corta a los ejes de coordenadas
 Matemáticas IES
Matemáticas IES