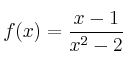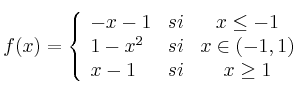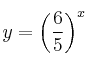EJERCICIOS RESUELTOS - Funciones
Mat. Aplicadas C. Sociales I - Funciones
Sea la función:
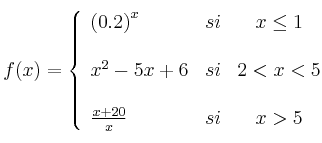
– a) Representación gráfica
– b) Indica Dominio, Corte con los ejes, Asíntotas, Monotonía y Extremos
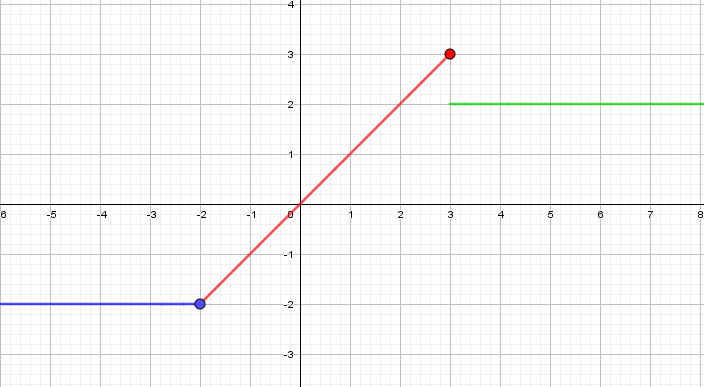
A continuación puedes ver la gráfica de una función definida a trozos. Obtén la expresión analítica, utilizando las expresiones adecuadas.
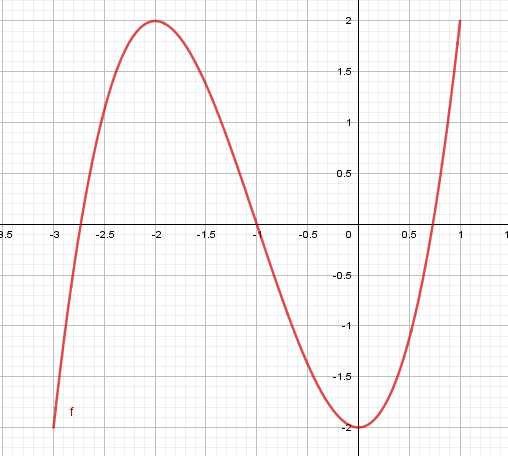
En la siguiente función indica:
a) Dominio
b) Recorrido
c) Extremos relativos (máximos y mínimos)
d) Puntos de corte. Si no coincide con un valor entero, utiliza una cifra decimal para expresarlo.
e) Monotonía (intervalos de crecimiento y decrecimiento)
Hallas asíntotas, puntos de corte con los ejes, dominio y rango de la función ![]() . Dibuja su gráfica.
. Dibuja su gráfica.
Dada la función 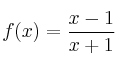 , se pide:
, se pide:
– a) Dominio, asíntotas, monotonía y corte con los ejes
– b) Representación gráfica
El beneficio esperado de una empresa, en millones de euros, viene dado por la función
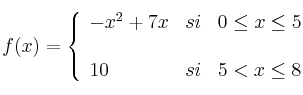
donde x representa el tiempo transcurrido en años.
– a) Representa gráficamente la función
– b) Explica cómo es la evolución del beneficio esperado durante esos 8 años y calcula cuándo el beneficio esperado es de 11,25 millones de euros.
Determina la monotonía y los extremos relativos de la función ![]()
 Matemáticas IES
Matemáticas IES